Definition of the Term Function

So, a function tells you how to match up one group of numbers with another group of numbers. For example, suppose 2 cans of soup cost $3.00. Then, 3 cans would cost $4.50, and 4 cans would cost $6.00. See how the numbers match up?

2 cans matches up with $3.00
3 cans matches up with $4.50
4 cans matches up with $6.00

Or, if you want to forget about what the numbers mean, then...

2 matches with 3.0
3 matches with 4.5
4 matches with 6.0

That rule for matching one certain number of cans with another certain number of dollars can be expressed in at least three ways.

(1) As a data table:

               Number of | Cost of
               Soup Cans | Soup
              -----------+---------
                   1     |  $1.50
                   2     |   3.00
                   3     |   4.50
                   4     |   6.00
                   5     |   7.50

(2) As a graph:

                    8.00 +
                         |              X
                         +
                         |
                    6.00 +           X
                         |
                         +
           Cost of       |        X
           Soup     4.00 +
                         |
             ($)         +     X
                         |
                    2.00 +
                         |  X
                         +
                         |
                    0.00 X--+--+--+--+--+--+
                         0     2     4     6

                         Number of Soup Cans

(3) Or, as an equation, here where the variable c stands for the cost of the soup, and the variable n stands for the number of soup cans:

                         c = 1.5n

INPUT and OUTPUT

Consider this simple function:

y = 2x

The variable x is where a number comes into the function. Therefore, we could call x the input variable.

The function rule says to multiply the number in x by 2 and then put this result, or output, into the variable y.

The variable y, therefore, could be called the output variable.

DOMAIN and RANGE

Again, consider this simple function:

y = 2x

The group, or set, of numbers that "goes into" a function is called the DOMAIN of the function.

The set of numbers that "comes out of" a function is called the RANGE of the function.

All of the various numbers that could possibly go into x make up the group of numbers called the domain of the function. In this example, since x could accept any real number, we would say that the domain of this function is all real numbers.

All of the various resultant numbers that end up in y make up the group of numbers called the range of the function. In this example there is exactly one real number that ends up in y for every one real number that went into x. So, we would say that the range of this function is also all real numbers.

Since x could be set equal to 3, we would say that the number 3 is in the domain of the function. The number 3 in x would be multiplied by 2, making a 6. This 6 would go into y. Since the 6 is output by the function, we would say that 6 is in the range of the function.

DOMAIN = INPUT NUMBERS = x
RANGE = OUTPUT NUMBERS = y

We have been looking at this function:

y = 2x

Notice that it has an equal sign in it, so it is an equation, or it could be called a relation.

However, not everything with an equal sign in it is a function.

Technically speaking, not every equation is a function. We need to find out when an equation is a function and when it is not.

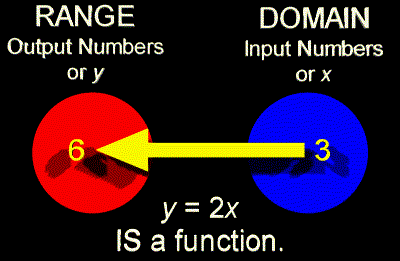
The above type of function has a special name.
It is called a ONE-TO-ONE FUNCTION.

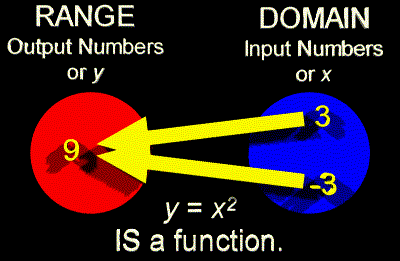
The above type of function also has a special name.
It is called a MANY-TO-ONE FUNCTION.

The above type of equation has a special name, too.
It is called a ONE-TO-MANY RELATION.

Be sure to understand that a one-to-many relation is not a function.

Below are several videos that will show you how ONE-TO-ONE FUNCTIONS, MANY-TO-ONE FUNCTIONS, and ONE-TO-MANY RELATIONS appear when they are seen as graphs. In each one the x-axis is shown in blue, the y-axis in red, the function (or relation) in yellow, and points and construction lines in white.

One-to-one Function

Many-to-one Function

One-to-many Relation