Parabola, Horizontal and Vertical Translations
Vertical and horizontal translations for the parabola can happen together using both h and k. So, our starting or reference parabola formula looks like this:
y = x2
And our equation that includes both a horizontal and vertical translation looks like this:
y = (x - h)2 + k
So, if h = 3 and k = 4, we say that the reference parabola is horizontally translated 3 units and vertically translated 5 units. Our equation for this would appear:
y = (x - 3)2 + 4
Here's the graph for these translations. The reference parabola ( y = x2 ) is drawn in transparent light gray, and the transformed parabola which is horizontally translated 3 units and vertically translated 4 units ( y = (x - 3)2 + 4 ) is drawn in black:
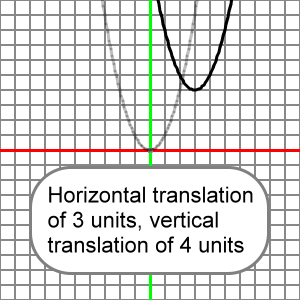
What follows is an animation that presents many horizontal and vertical translations for our reference parabola.
Please understand that x^2 means x2.

We see here how the horizontal and vertical translations of the reference parabola can occur within the same formula. Here is a calculation for the y-coordinate of the transformed parabola when the reference parabola is horizontally translated to the right 3 units and vertically translated downward 4 units. We will work at x = 5:
y = (x - h)2 + k
y = (5 - h)2 + k
y = (5 - 3)2 + (-4)
y = (5 - 3)2 - 4
y = 22 - 4
y = 4 - 4
y = 0
Here is an EZ Graph example of these vertical and horizontal translations. Press the 'Draw Graph' button.
You can change the value for h or k using the upper left input boxes. Press the 'Draw graph' button after you change h or k, and you will see how your change effects the graph. For more information about EZ Graph click the following link: