Parabola, Horizontal Translation

Horizontal translation for the parabola is changed by the value of a variable, h, that is subtracted from x before the squaring operation. So, our starting or reference parabola formula looks like this:

y = x²

And our equation that includes a horizontal translation looks like this:

y = (x - h)²

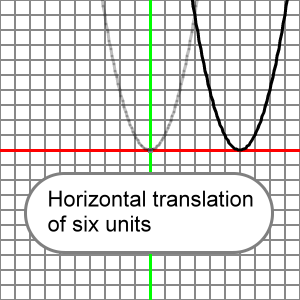
So, if h = 6, we say that the reference parabola is horizontally translated by 6 units, and our equation for this would appear:

y = (x - 6)²

Here's the graph for this translation. The reference parabola ( y = x² ) is drawn in transparent light gray, and the transformed parabola which is horizontally translated 6 units ( y = (x - 6)² ) is drawn in black:

What follows is an animation that presents many horizontal translations for our reference parabola. Note that the value for h is subtracted from x, and then this difference is squared. See that positive values for h translate the parabola to the right, negative values for h translate the parabola to the left.  When h = 0, the reference and transformed parabola would be the same.

Please understand that x^2 means x².

It may not seem correct at first that you must subtract from x to move the parabola to the right, but that is how it works. Subtractions on the x-axis are usually related with movements to the left, but not here. If you want to move the parabola to the right, say, 4 units, then you must subtract 4 from x and then square that result to get your y-coordinate.

Be sure to understand that the subtraction from x occurs before the squaring. Imagine that we translate the reference parabola 3 units to the right. Let's see what is the y-coordinate at x = 5:

y = (x - h)²

y = (x - 3)²

y = (5 - 3)²

y = (2)²

y = 4

How do you translate the reference parabola to the left? Well, you subtract a negative number from x. This looks like an addition to x. Let's calculate the y-coordinate on our transformed parabola when we translate the reference parabola 6 units to the left. We will calculate at x = 2:

y = (x - h)²

y = (x - (-6))²

y = (2 - (-6))²

y = (2 + 6)²

y = (8)²

y = 64

So, if you wish to move the reference parabola to the right, subtract a positive number from x.

If you want to move the reference parabola to the left, subtract a negative number from x. Since we are subtracting a negative number, this could look like an addition. Here's an example:

Subtracting a negative number from x:

y = (x - (-3))²

Can look like an addition:

y = (x + 3)²

So, a graph of this function:

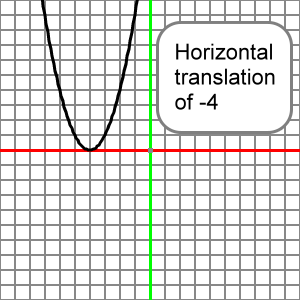
y = (x + 4)²

Which we should think of as:

y = (x - (-4))²

Would look like the reference parabola shifted to the left 4 units:

And a graph of this function:

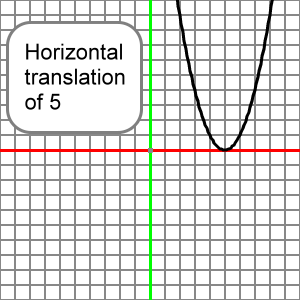
y = (x - 5)²

Would look like the reference parabola slid to the right 5 units:

Here is an EZ Graph example of this horizontal translation. Press the 'Draw graph' button.

You can change the value for h using the upper left input boxes. Press the 'Draw graph' button after you change h, and you will see how your change effects the graph. For more information about EZ Graph click the following link:

Help with EZ Graph