Parabola, Vertical Translation

Vertical translation for the parabola is changed by the value of a variable, k, that is added into the calculation for y after x is squared. So, our starting or reference parabola formula looks like this:

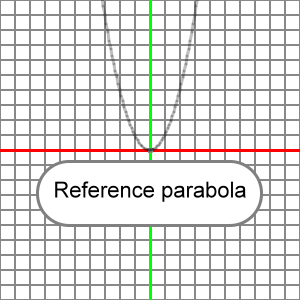
y = x²

And our equation that includes a vertical translation looks like this:

y = x² + k

So, if k = 5, we say that the reference parabola is vertically translated by 5 units, and our equation for this would appear:

y = x² + 5

Here's the graph for this translation. The reference parabola ( y = x² ) is drawn in transparent light gray, and the transformed parabola which is vertically translated 5 units ( y = x² + 5 ) is drawn in black:

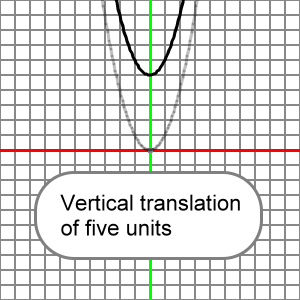
What follows is an animation that presents many vertical translations for our reference parabola. Note that the value for k is added into the calculation for y after x is squared. See that positive values for k translate the parabola to the up, negative values for k translate the parabola to the down.  When k = 0, the reference and transformed parabola would be the same.

Please understand that x^2 means x².

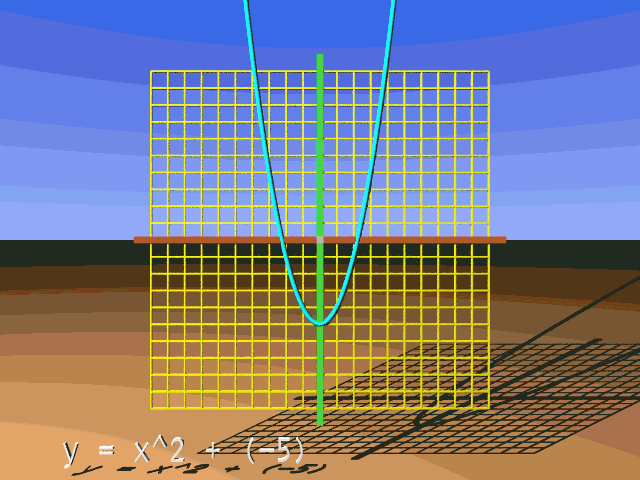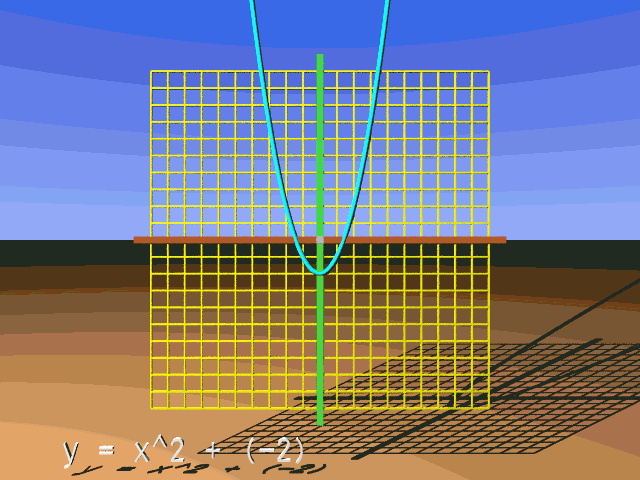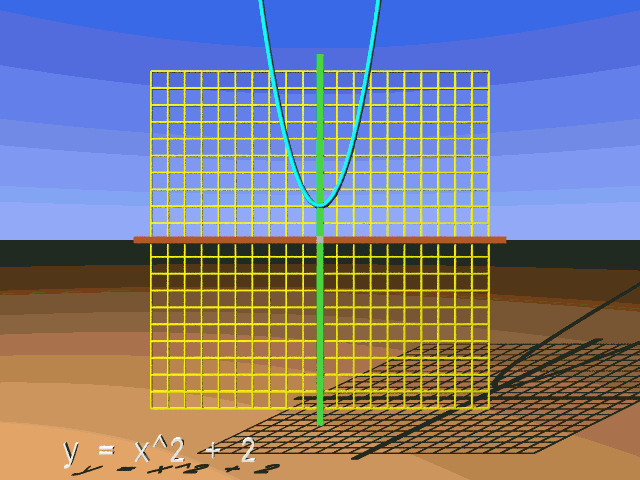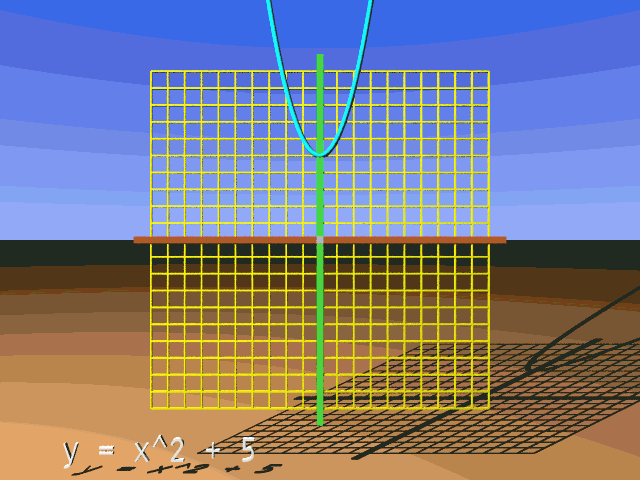
It is easy to see how this vertical translation moves the reference parabola up or down. Let us do a simple calculation that will get us from the reference parabola to the transformed, vertically translated parabola. We will work at x = 3 and make a vertical translation upward of 4 units. First, what would be the y-coordinate on the reference parabola at x = 3? Here's the calculation:

y = x²

y = 3²

y = 9

 Now, notice the formula for the transformed parabola with a vertical translation:

y = x² + k

Since the squaring of x occurs before the addition of k, the y-coordinates of the transformed, vertically translated parabola are simply the corresponding y-coordinates of the reference parabola with k added to them. If k is positive, this lifts the y-coordinates up. If k is negative, this moves them down.

Here's the calculation for the y-coordinate on the transformed, vertically translated parabola at x = 3. Let's imagine the the translation to be 5 units:

y = x² + k

y = 3² + k

y = 3² + 5

y = 9 + 5

y = 14

Hopefully, it is clear that on this transformed, vertically translated parabola at x = 3 we simply have the reference y-coordinate, 9, with 5 added to it, lifting the reference parabola up 5 units to land on the transformed parabola. A similar lift happens at each x-coordinate.

To transform the reference parabola down, we make k negative. This can look like a subtraction. Let's work at x = 5 and perform a vertical translation downward of 3 units. So, k = -3. Here's the calculation for the y-coordinate:

y = x² + k

y = 5² + k

y = 5² + (-3)

y = 5² - 3

y = 25 - 3

y = 22

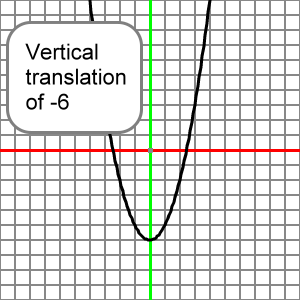
Let's look at the graph of this function:

y = x² - 6

Which we think of as:

y = x² + (-6)

This should look like the reference parabola translated downward 6 units:

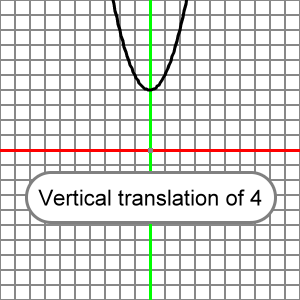
This function:

y = x² + 4

Will look like the reference parabola translated up 4 units:

Here is an EZ Graph example of this vertical translation. Press the 'Draw graph' button.

You can change the value for k using the upper left input boxes. Press the 'Draw graph' button after you change k, and you will see how your change effects the graph. For more information about EZ Graph click the following link:

Help with EZ Graph