Total Surface Area and Volume of a Box
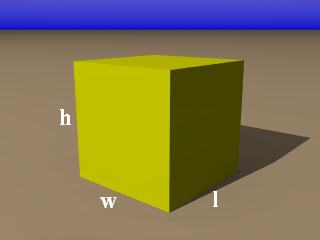
The total surface area is made up of three pairs of sides for a total of six sides.
We must find Areahw, which is the area of the side that is h by w.
Areahw = (h)(w)
We must find Areahl, which is the area of the side that is h by l.
Areahl = (h)(l)
We must find Areawl, which is the area of the side that is w by l.
Areawl = (w)(l)
Each of the above areas are present on two sides of the box. So, the total surface area is sum of twice each of these areas, that is:
Total Surface Area = 2(Areahw) + 2(Areahl) + 2(Areawl)
The volume of the box is simply the product of h, w, and l.
Volume = (h)(w)(l)
Example:
Let h = 3 cm, w = 5 cm, l = 8 cm
Areahw = (h)(w) = (3 cm)(5 cm) = 15 cm2
Areahl = (h)(l) = (3 cm)(8 cm) = 24 cm2
Areawl = (w)(l) = (5 cm)(8 cm) = 40 cm2
Total Surface Area = 2(Areahw) + 2(Areahl) + 2(Areawl)
Total Surface Area = 2(15 cm2) + 2(24 cm2) + 2(40 cm2)
Total Surface Area = 30 cm2 + 48 cm2 + 80 cm2
Total Surface Area = 158 cm2
Volume = (h)(w)(l)
Volume = (3 cm)(5 cm)(8 cm)
Volume = 120 cm3