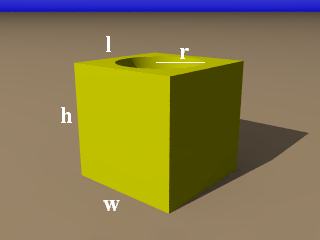
Total Surface Area and Volume of a Box with a Cylindrical Hole

Be sure you understand how to find the total surface area and volume of a box and of a cylinder before going ahead here.

The total surface area of this new shape is made up several areas, some like parts of the box, some like parts of the cylinder, and some like differences between parts of the box and cylinder.

Like the box, this shape has a pair of sides with areas which we will again call Area_hw.

Like the box, this shape also has another pair of sides with areas which we will again call Area_hl.

The top and bottom of this shape form another pair of equal areas. These areas are both equal to the area of the top of the box after a circular hole has been cut out of it. This hole has an area equal to the area of the circular top of the cylinder. So, the area of the top of this shape is calculated this way:

The area of the top of the box is Area_lw, so, restating the above:

Again, we have two areas, top and bottom, that are equal to the immediate above value.

In this shape the area of the side of the hole is like the area of the side of the cylinder, so:

So, the total area of this shape is equal to:

The volume of this shape is the volume of the box, as calculated before, minus the volume of the cylindrical hole, also as calculated before.