Intersection of Two Parabolas

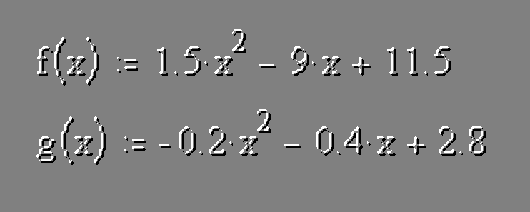
We will cover a method for finding the point or points of intersection for two quadratic functions. Quadratic functions graph as parabolas. So, we will find the (x, y) coordinate pairs where the two parabolas intersect.

First, understand that two parabolas may intersect at two points, as in these pictures:

Or, the parabolas may intersect at only one point, as in these pictures:

Or, they may not meet at any points, as shown here:

Our example will use these two quadratic functions:

f(x) = 1.5x²- 9x + 11.5

g(x) = -0.2x²- 0.4x + 2.8

Of course, quadratic functions, or second degree polynomial functions, graph as parabolas. Since we will be graphing these functions on the x, y coordinate axes, we can express the parabolas this way:

y = 1.5x²- 9x + 11.5

y = -0.2x²- 0.4x + 2.8

Those two parabolas look this way:

Now, where the two parabolas cross is called their points of intersection. Certainly these points have (x, y) coordinates, and at the points of intersection both parabolas share the same (x, y) coordinates. So, at the points of intersection the (x, y) coordinates for f(x) equal the (x, y) coordinates for g(x).

Since at the points of intersection the y-coordinates are equal, (we'll be working with the x-coordinates later), let's set the y-coordinate from from one parabola equal to the y-coordinate from the other parabola.

The y-coordinate for f(x) is calculated this way:

y = 1.5x²- 9x + 11.5

The y-coordinate for g(x) is calculated this way:

y = -0.2x²- 0.4x + 2.8

Setting the two y-coordinates equal to each other creates this equation:

1.5x²- 9x + 11.5 = -0.2x²- 0.4x + 2.8

Now, we do some algebra to find the x-coordinates at the points of intersection:

	This is where we start.
	Subtract 1.5x2 from each side.
	Add 9x to each side.
	Subtract 11.5 from each side. This leaves us with a quadratic equation.
	Use the quadratic formula to solve for x.
	These are the x-coordinates for the two points of intersection. (The values her are truncated to two decimal places and not rounded.)

So, we have the x-coordinates for the points of intersection. They are x = 1.39 and x = 3.66. Now, let's find the y-coordinates. Each y-coordinate can be found by placing its corresponding x-coordinate into either of the equations for the parabolas and solving for y. We will first use the equation from the first parabola. Here we plug x = 1.39 into it:

y = 1.5x² - 9x + 11.5

y = 1.5(1.39)² - 9(1.39) + 11.5

y = 2.89 - 12.51 + 11.5

y = 1.88

So, one point of intersection is very close to (1.39, 1.88). Here, we say very close to since the values have been calculated using only two decimal places.

Now, plugging in the other x-coordinate into the equation for the first parabola, we can get the other y-coordinate for the second point of intersection:

y = 1.5x² - 9x + 11.5

y = 1.5(3.66)² - 9(3.66) + 11.5

y = 20.09 - 32.94 + 11.5

y = -1.35

The other point of intersection is very near (3.66, -1.35).

Here are these points of intersection shown on the graph of the two parabolas:

The above procedure can be used to find the intersection of any two parabolas. Of course, the parabolas will not always intersect at two points. Sometimes they will only intersect at one point, and quite often they will not intersect at all. These conditions will show up when you solve the quadratic equation after you set the two separate functions equal to each other and collect like terms. When solving that quadratic equation, if the discriminant equals zero, then you will have only one solution for x, which boils down to only one point of intersection. If the discriminant is negative, then there are no solutions for x, which means the two parabolas do not intersect.

Ready to try it yourself? Below is a calculator which you can use to check your work. First, make up two second degree polynomial functions, (quadratic functions), in this form:

y = ax² + bx + c

You could use the function grapher in the Function Institute to help you find the values for a, b, and c, or you could just make them up. Perhaps for one of your parabolas you would choose:

y = 1.5x² - 9x + 11.5

If you wanted to see this function using EZ Graph you would type this into one of the 'y =' boxes at the bottom:

1.5*x^2 - 9*x + 11.5

(Don't forget to check the 'Use' box before clicking the 'Draw' button.)

At any rate, get yourself two parabolic functions, use the method above to find their intersections, and then put the values for a, b, and c for each parabola into the calculator below, click 'Calculate intersections' and check your work.