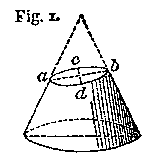Conic Sections

A conic section is a section of a cone. The ellipse, parabola, and hyperbola, along with a few other mathematical shapes, can each be shown to be a section of a cone.

In our context here, a cone is thought to be a hollow cone, quite a bit like the 'sugar cones' in an ice cream shop. So, these mathematical cones look like this one to the left.

And actually when thinking about conic sections, we envision two such cones lined up vertically tip to tip. So, conic section cones in mathematics appear as shown to the left.

Although the cones in this picture seem to have some finite height (from tip to base), we must think of these cones as extending on forever without a top or bottom limit (base).

Such a pair of cones is formally called a circular conical surface, and a discussion of conic sections is centered around this surface.

A line which we imagine running through the center of the cones in a direction perpendicular to their bases is called the axis. This is shown to the left.

Now, about the 'section' word in the term 'conic section'. This section is a very thin slice of the cones. In fact, it is an infinitely thin slice.

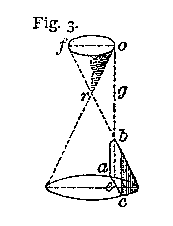
Think of the cones as being sliced by a plane. So, we speak about the intersection of the cones with a plane. The shape of this intersection is the shape of the conic section. To the left is one example of how we could imagine a cone being intersected by a plane. (Remember, both the cone and the plane actually extend to infinity.)

The shape of the intersection, or cut, that the plane makes with the cone is the shape of the conic section. For example, in the above picture the intersection is a hyperbola.

The way in which the plane cuts through the cones determines the shape of the intersection, and thus determines the particular conic section. It determines if the conic section is a parabola or ellipse, and so on. Several ways in which a plane can intersect the cone are illustrated in the following video. (This and other videos may show cones with bottoms rather than showing hollow cones.)

To see how the plane and cone, (or circular conical surface), intersect to form a particular conic section, click on one of the links below.

The following are actually special cases, or degenerate cases, of conic sections: