Where does the quadratic formula come from?

First of all, let us be sure we understand what is meant by the term quadratic formula. To do that, we must understand what is meant by the terms quadratic expression and quadratic equation.

A quadratic expression is a polynomial of this form:

A quadratic equation is an equation of the form:

Examples of quadratic equations would be:

When equations of this form are solved for x, you get you get the quadratic formula, which is:

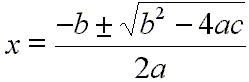
That is, you can use this calculation to find the values of x that make the quadratic equation equal to zero. These specific values of x are called the roots of the quadratic equation. They are also called the zeros of the equation.

A calculator for solving the quadratic formula is available here. However, proceed below if you want to know how the above equation that solves for x is derived.

Let us figure out why x is equal to the above value. First, start with the quadratic formula:

Subtract c from both sides to get:

Divide both sides by a:

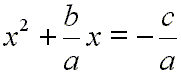
This next step may look a bit mysterious at first. It will allow us to turn the left side of the above equation into a perfect square. This method of turning one side of an equation into a perfect square is often called 'completing the square'.

Add 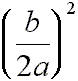to both sides:

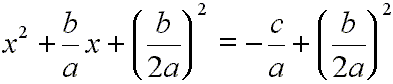
Factor the left side of this equation by asking this question:

What two numbers when added are and when multiplied are ?

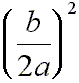That number is .

Therefore, we can see the left side of [4] as a perfect square that factors this way:

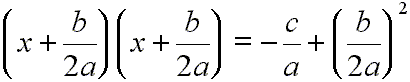
The left side can now be written this way:

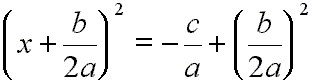
Let us do a bit of algebra on the right side of [6]:

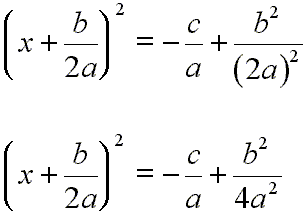
Now, we get a common denominator on the right side:

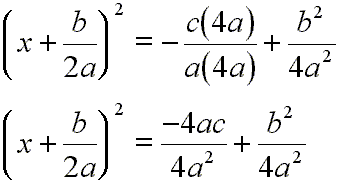
Adding on the right side:

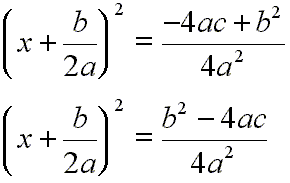
Taking the square root of each side:

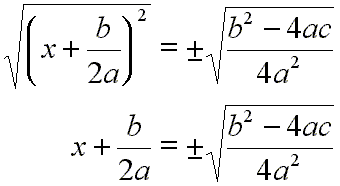
Subtract from each side:

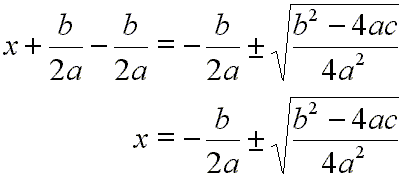
Do some algebra on the right side:

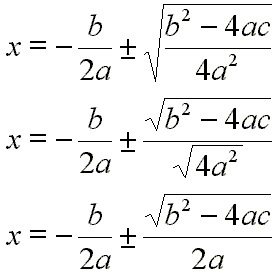
Since the terms on the right side now have a common denominator, we will combine those terms by adding them:

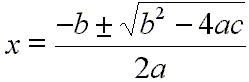
And we are all done. [13] is the solution to the quadratic equation.

A calculator for solving the quadratic formula is available here.