45-45-90 and 30-60-90 Triangles
This page summarizes two types of right triangles which often appear in the study of mathematics and physics.
One of these right triangles is named a 45-45-90 triangle, where the angles in the triangle are 45 degrees, 45 degrees, and 90 degrees. This is an isosceles right triangle.
The other triangle is named a 30-60-90 triangle, where the angles in the triangle are 30 degrees, 60 degrees, and 90 degrees.
Common examples for the lengths of the sides are shown for each below.
The 45-45-90 Triangle
 |
Here we check the above values using the Pythagorean theorem. The length of the hypotenuse should be equal to the square root of the sum of the squares of the legs of the triangle. |
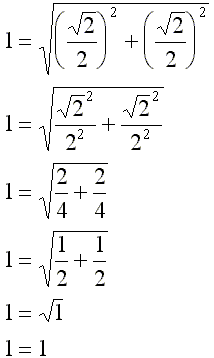 |
Listed below are the values shown in the diagram as well as another common set of values for this triangle. Be sure to notice that the two legs have the same length, so, the leg length is listed only once.
| Hypotenuse Length |
Leg Length |
| 1 | 0.7071 |
| 1.4142 | 1 |
The 30-60-90 Triangle
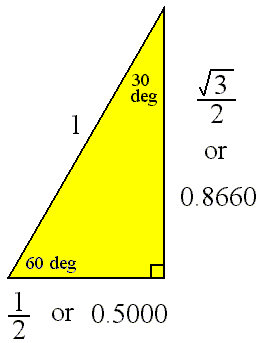 |
Here we check the above values using the Pythagorean theorem. The length of the hypotenuse should be equal to the square root of the sum of the squares of the legs of the triangle. |
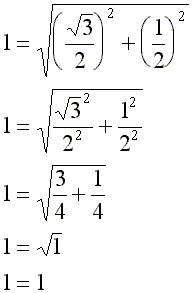 |
Listed below are the values shown in the diagram as well as another common set of values for this triangle.
| Hypotenuse Length |
Leg Length Opposite 30 Deg |
Leg Length Opposite 60 Deg |
| 1 | 0.5000 | 0.8660 |
| 2 | 1 | 1.7320 |
| 1.1547 | 0.5773 | 1 |