Types of Numbers
This is a Venn diagram that shows the relationships between different types of numbers:
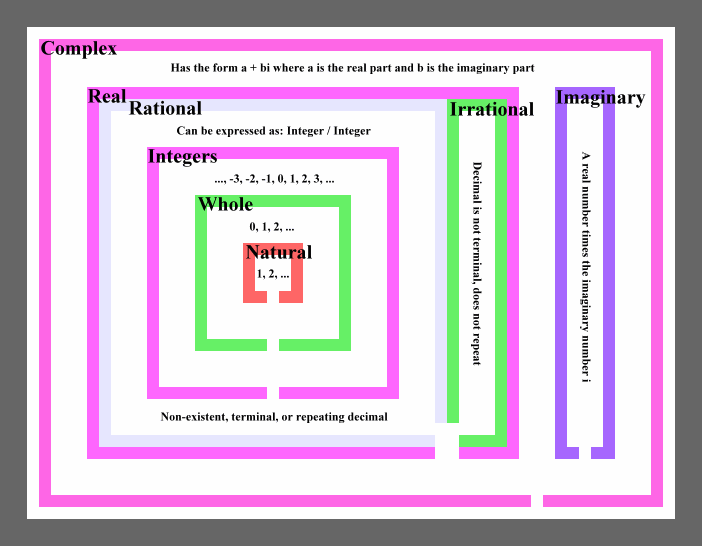
The types of numbers are:
- Complex numbers
- Complex numbers with both a real and imaginary part
- Imaginary numbers; that is, complex numbers with no real part.
- Real numbers; that is, complex
numbers with no imaginary part
- Rational numbers
- Integers
- Whole numbers
- Natural numbers
- Irrational numbers
- Rational numbers
Here is a brief description of each of the above types of numbers, starting with the Natural Numbers:
Natural Numbers
This group of numbers starts at 1. It includes 1, 2, 3, 4, 5, and so on. Zero is not in this group. This group has no negative numbers. There are no numbers with decimals in this group.
Natural numbers could be seen as:
1, 2, 3, 4, 5, ....
Whole Numbers
This group has all of the Natural Numbers in it plus the number 0.
Whole numbers could be seen as:
0, 1, 2, 3, 4, 5, ...
Integers
This group has all the Whole Numbers in it and their opposites, or, you might say, and their negatives.
Integers could be see as:
... -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ...
Rational Numbers
This is any number that can be expressed as a ratio of two integers. Note the ratio in rational.
Often this group is defined in terms of how the decimals act. That is, the decimals either do not exist, as in 5, (which is 5/1). Or the decimals terminate, as in 2.4, (which is 24/10). Or the decimals repeat with a pattern, as in 2.333..., (which is 7/3). This way of defining a rational number, however, really misses the point. The behavior of the decimals is just fallout that you get when you divide an integer by another integer.
Irrational Numbers
This is any number that can not be express as an integer divided by an integer, (not counting, no pun intended, imaginary or complex numbers).
These numbers have decimals that never terminate and never repeat with a pattern.
Examples include pi, e, and the square root of two.
Real Numbers
This group is made up of all the Rational and Irrational Numbers. The ordinary number line encountered when studying algebra holds real numbers.
Imaginary Numbers
These are all based on the imaginary number i. This imaginary number is equal to the square root of negative one. Any real number times i is an imaginary number.
Examples include i, 3i, -9.3i, and (pi)i.
Complex Numbers
A Complex Numbers is a combination of a real number and an imaginary number in the form a + bi. The real part is a, and b is called the imaginary part.
Examples include 4 + 6i, 2 + (-5)i, (often written as 2 - 5i), 3.2 + 0i, and 0 + 2i.
Note the last two examples:
3.2 + 0i is just the real number 3.2. All real numbers are complex numbers with zero for the imaginary part.
0 + 2i is just the imaginary number 2i. All imaginary numbers are complex numbers with zero for the real part.