The Radian

The word radian describes a certain size of an angle. In the animation below the blue pie slice shape demonstrates an angle of one radian. Notice that for an angle of one radian the arc length along the edge of the circle is equal in length to the radius. Read the details below...

Usually, a person first learns how to measure the size of an angle using degrees. There are, of course, 360 degrees all the way around a circle.

The degree, however, turns out to be not a very mathematical way of measuring angles. The radian is used much more than the degree in higher mathematics for measuring angles.

A radian is defined this way:

If you have a circle with an angle whose vertex is at the center of that circle...
And if that angle is of such a size that the amount of the circumference of the circle which that angle intercepts has an arc length equal to the length of the radius...
Then that angle has a measurement of one radian.

Here's another way to say it:

A central angle to a circle has a size of one radian if it subtends an arc length on the circle equal in length to the radius.

In other words, if you could pick up the radius of a certain circle like it were a plastic rod and bend it around the circumference of that circle, then that bent radius length would touch the sides of a central angle which had a measurement of one radian. Look at the following picture and then go back and look at the animation.

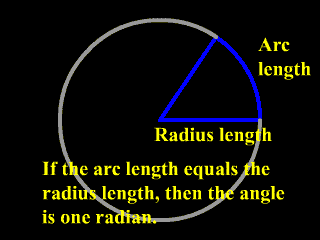
radian angle in circle

One thing to understand about a radian is that it is bigger than a degree. In fact:

1 radian = 57.2957 degrees

1 degree = 0.0174532 radians

The above values are to six significant figures, truncated, not rounded. If you want to know the exact size of the radian in terms of degrees, take 360 and divide it by 2 times pi. That number is how many degrees there are in a radian.

What is the reasoning behind these values? It works this way:

How many times can you trace an arc length equal to the size of the radius as you move around the circumference of a circle? Well, here's the formula for the circumference of a circle:

C is the circumference, and r is the radius.

The formula reads: 'The circumference equals two times pi times the radius.'

Looks like there are two pi radii around the circumference of a circle, or about 2 times 3.14, i.e., about 6.28, radii around the circumference of a circle. Each one of these radius lengths would designate one radian, so there are about 6.28 radians in a full circle. The following diagram shows this:

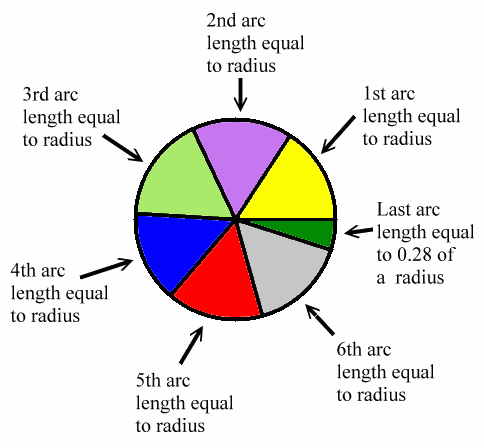
diagram demonstrates two pi radians are around a circle

Therefore, there are 2 pi radians in a full circle.

We also know that there are 360 degrees in a circle.

So, there are 360 degrees per 2 pi radians. Dividing 360 by 2 pi give us the value of about 57.2957 degrees per radian. A radian is equal to 57.2957 degrees.

Also, by dividing 2 pi radians by 360 degrees we get about 0.0174532 radians per degree. A degree is equal to 0.0174532 radians.

In mathematics if you state the size of an angle as a pure number, without the degree 'unit' marker after it, then the angle is taken to be in radians. So, if the angle in question is named A, and if someone were to write down:

A = 4

Then that would mean that angle A has a measurement of 4 radians and not 4 degrees.