Ray Optics, Snell's Law

Willebrord Snell discovered the law of refraction which we now call Snell's law.
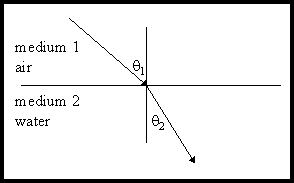
Let us look at a simple refraction, one where a light ray travels from air into water:
Conventions in the above diagram work this way:
- The incident medium, air in this case, is called the first medium, or medium 1.
- The angle of incidence is named with the Greek letter theta, and, since it is in medium 1, is called theta1.
- The refracted medium, water in this case, is called the second medium, or medium 2.
- The angle of refraction, again named with the Greek letter theta, is called theta2.
In the above diagram approximate values for the angles are:
theta1 = 43 degrees
theta2 = 31 degrees
Now, if you divide the sine of theta 1 by the sine of theta 2 you get:
sin(43 degrees) / sin(31 degrees) = 1.32
In actual practice, using exact values for the angles, you would get:
sin(theta1) / sin(theta2) = 1.33
As it turns out, this ratio is always equal to 1.33 for any angle of incidence and its corresponding angle of refraction. This is our first look at Snell's law.
For a light ray going from air into water, the sine of the angle of incidence divided by the sine of the angle of refraction is constant, that is, this ratio is always equal to the same value:
sin(theta1) / sin(theta2) = is a constant = 1.33
Now, this constant has a name and a symbol.
The name is "the absolute index of refraction for water." Usually, this is shortened to "the index of refraction of water."
The symbol is nwater.
So, we say that the index of refraction for water is 1.33, or nwater = 1.33.
Obviously, if you know, say, the angle of incidence, and you know that the light ray is going from air into water, then you can find the angle of refraction. For example, if the angle of incidence was 25 degrees:
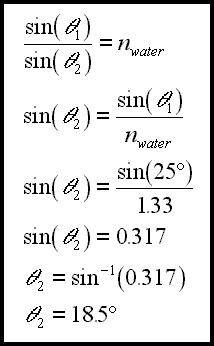
The angle of incidence is 25 degrees.
The light is going from air into water.
nwater = 1.33
So, the angle of refraction calculates to be 18.5 degrees.
As it turns out, this whole discussion could have been done with the light ray going from air into glass. Everything would be the same, except we would no longer be speaking about the index of refraction for water, we would be speaking about the index of refraction for glass. The index of refraction for glass is 1.50. So, for light going from air into glass:
sin(theta1>) / sin(theta2) = constant = nglass = 1.50
Every substance has its own index of refraction. Here are a few examples:
| Water | 1.33 |
| Glass | 1.50 |
| Quartz crystal | 1.54 |
| Glycerin | 1.47 |
| Diamond | 2.42 |
These indices of refraction could each be found by sending a light ray from air into the substance, measuring the angle of incidence and the angle of refraction, and then dividing the sine of the angle of incidence by the sine of the angle of refraction.
And now for some fine points:
The index of refraction for glass can be between 1.50 and 1.90 depending upon how the glass is made. For most introductory physics problems an index of 1.50 is used.
To actually find the absolute index of refraction for a substance as described above, the light ray can not go, say, from air into water. It must go from a perfect vacuum, often called free space, into water. This, of course, is experimentally impossible. However, light travels through air much like it travels through free space. It moves a very tiny percent slower. As you'll see below, the index of refraction is tied to the velocity of light in the different mediums. Since light's velocity is about the same in free space and air, discussing the absolute index of refraction as we have done is not all that bad - as long as one understands the fine point.
Free space would have an index of refraction of 1.00. So, what is the index of refraction for air? That is, what would you get for this value if you could send a light ray from a perfect vacuum into air? Well, for most introductory physics problems consider the index of refraction for air to be 1.00. Actually it is ever so slightly larger than 1.00, and, different densities of air have slightly different indexes of refraction. That's why the light beams bend up looking like ripples when your vision skims across a hot object, like a highway. The air near the surface goes into mild turbulence due to heating. It contains dynamic pockets of air at different temperatures, and, thus, at different pressures, and, thus, with slightly different indices of refraction. Light rays traveling through this air turbulence are refracted a bit chaotically, and the rippling vision results.
And now, a not so fine point:
Truly, a complete understanding of Snell's law does not define the index of refraction of a substance as the ratio of the sine of the angle of incidence to the sine of the angle of refraction. It defines the index of refraction as the speed of the light in free space divided by the speed of the light in the substance.
This ratio of speeds happens to give the same value for the index as the ratio of the angles described above. So, since the speed of light in air is almost exactly equal to the speed of light in a vacuum, we could state our current version of Snell's law, say, for light going from air into water, this way:
vair / vwater = sin(theta1) / sin(theta2) = nwater = 1.33
Notice that now, knowing the speed of light in air, which is about equal to the speed of it in free space, or 300,000,000 m/s, and knowing the index of refraction for a substance, one could find the speed of light in that substance, as in:
vsubstance = vair / nsubstance
Or:
vsubstance = (300,000,000 m/s) / nsubstance
And that concludes our first understanding of Snell's law. In summary, we will say:
- Every material that light can travel through has an absolute index of refraction. This value is usually simply termed "the index of refraction" for that substance.
- The index of refraction for a substance is equal to the speed of light in free space divided by the speed of light in that substance.
- The index of refraction for a substance is also equal to the sine of the angle of incidence, in free space, divided by the sine of the angle of refraction, in the substance.
- For all practical purposes, in introductory physics problems like these, one can consider light to move through air much like it moves through free space. However, it actually travels a bit slower in air.