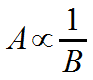Inverse Proportion and The Hyperbola Graph

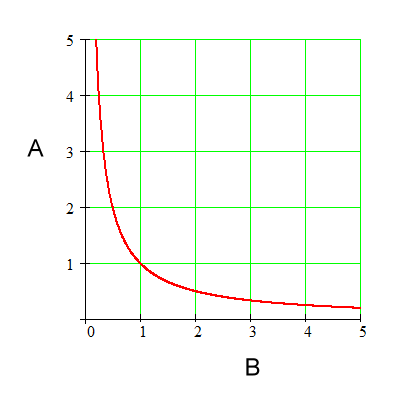
Hyperbola graphs, like the one immediately below, show that the quantities on the graph are in inverse proportion. This graph states, therefore, that A is inversely proportional to B. (It also states that B is inversely proportional to A, but we are going to work with the statement 'A is inversely proportional to B'.)

inverse proportion graph, the hyperbola

For the above graph:

A alpha one over B

This is how you write an inverse proportion. The symbol in the middle is the Greek letter alpha.

It reads: A is inversely proportional to B.

It means: By whatever factor A changes, B changes by the inverse of that factor. (Or you could say, “by the reciprocal of that factor”.)

Well, let's examine the graph and find out if its shape is such that A and B change by inverse factors.

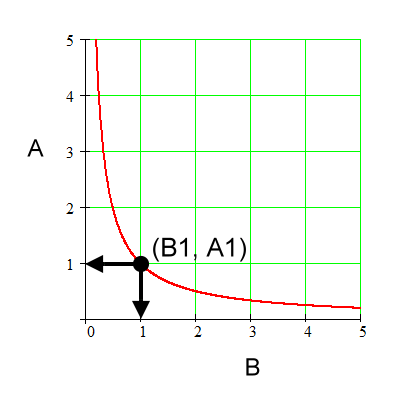
Below is an example of a point on this graph. The point is (B1, A1) and it has coordinates (1, 1).

A vs. B graph, coordinates for (B1, A1)

For the above graph:

	Coordinate for B1.
	Coordinate for A1.

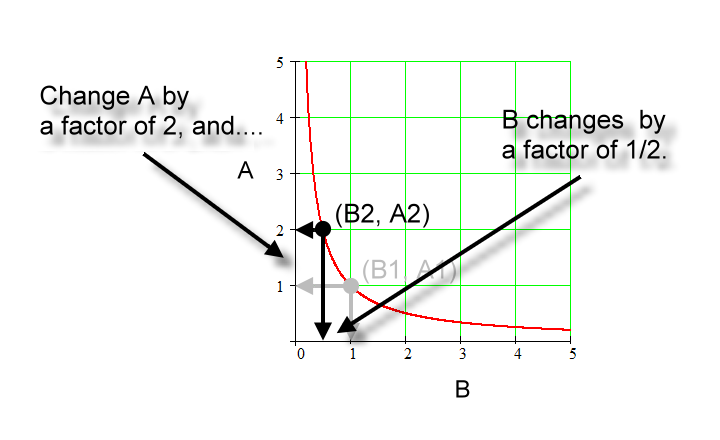
We will check for this hyperbola shape of a graph if we change A by some factor, does B truly change by the inverse factor, thus showing that this hyperbola shape represents an inverse proportion.

Here's what we are looking for:

A changes by a factor of two, B changes by a factor of one half.

The explanation:

In the graph below we go from 'sub 1' to 'sub 2' and change the quantity A by a factor of 2; that is, we double it.

A vs. B graph, coordinates for (B2, A2)

For the above graph:

	Coordinates for (B1, A1).
	Coordinates for (B2, A2).
	Going from 'sub 1' to 'sub 2', A changes by a factor of 2. That is, A1 times a factor of 2 equals A2.
	Going from 'sub 1' to 'sub 2' B, changes by a factor of 1/2. B1 times a factor of 1/2 equals B2.
	A and B change by the inverse factors. Those factors are 2 and ½ respectively.
	Therefore, A is inversely proportional to B.

So, again:

A vs. B graph showing reciprocal factor changes for A and B

Let's try this again below for another point using the same graph. Here's where we are headed:

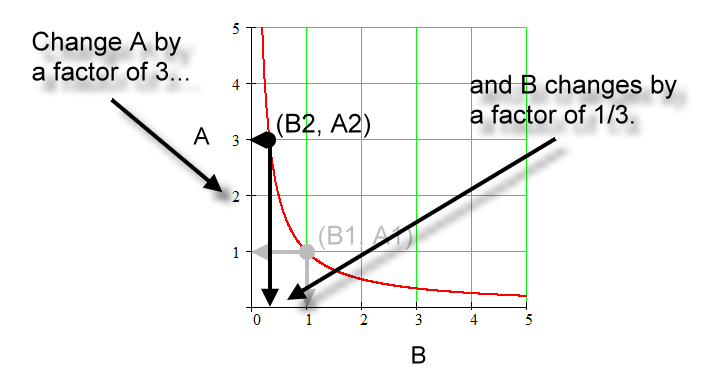
A vs. B graph showing reciprocal factor changes for A and B

The steps follow as we move from 'sub 1' to 'sub 2':

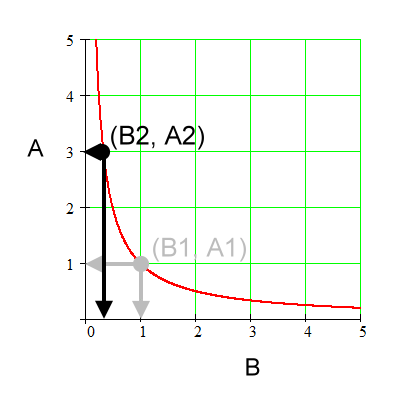
A vs. B graph showing coordinates for (B2, A2)

For the above graph:

	Coordinates for (B1, A1).
	Coordinates for (B2, A2).
	Going from 'sub 1' to 'sub 2', A changes by a factor of 3.
	Going from 'sub 1' to 'sub 2', B changes by a factor of 1/3.
	A and B change by inverse factors. Those factors are 3 and 1/3 respectively.
	Therefore, A is inversely proportional to B.

Here's the picture once more:

A vs. B graph showing reciprocal factor changes for A and B

And again, if A is inversely proportional to B, then B is inversely proportional to A. The logic works out the same.

The function on the graph is:

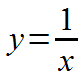
y equals one over x

Or, using a formal function definition:

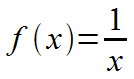
f of x equals one over x

Lastly, this:

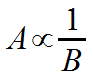
A alpha one over B

could probably be read 'A is directly proportional to the inverse of B', but that would be unusual. It's 'A is inversely proportional to B'.