Projectile Motion, General Solution
What follows is a general solution for the two dimensional motion of an object thrown in a gravitational field. This is usually termed a projectile motion problem. The thrown object is called the projectile. Its path is called the trajectory.
We will answer all the usual questions that arise in a first year physics class regarding this motion. We will not consider air resistance. Without air resistance, the projectile will follow a parabolic trajectory. We will be throwing the projectile on level ground on planet Earth. It will leave the point of release, arc through the air along a path shaped like a parabola, and then hit ground a certain distance from where it was thrown.
As mentioned above, this is a two dimensional problem. Therefore, we will consider x- and y-directed displacements, velocities, and accelerations.
The projectile will accelerate under the influence of gravity, so its y-acceleration will be downward, or negative, and will be equal in size to the acceleration due to gravity on Earth.
There will be no acceleration in the x-direction since the force of gravity does not act along this axis.
On Earth the acceleration due to gravity is 9.8 m/s2 directed downward. So, for this presentation acceleration in the y-direction, or ay, will be -9.8 m/s2, and acceleration in the x-direction, or ax, will be 0.0 m/s2.
| Two dimensional acceleration: | 9.8 m/s2, downward |
| X-acceleration: | 0 m/s2 |
| Y-acceleration: | -9.8 m/s2 |
Given the original conditions with which the projectile is thrown we will proceed to find the components of the original velocity and then move on to answer the following questions:
- How much time passes till the projectile is at the top of its flight?
- How high does the projectile rise?
- How much time passes till the projectile strikes the ground?
- How far away does the projectile land from its starting point?
Original, or initial, conditions:
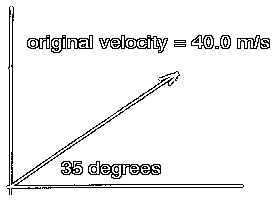
The original conditions are the size of the velocity and the angle above the horizontal with
which the projectile is thrown.
General:
Original size of velocity: vo
Original angle: theta
Example:
vo= 40.0 m/s
theta = 35 degrees
Components of original velocity:
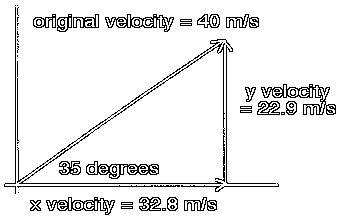
The usual first step in this investigation is to find the x- and y-components for the original velocity.
General:
X-component of original velocity: vox= vocos(theta)
Y-component of original velocity: voy= vosin(theta)
Example:
In the x-direction:
vox= vocos(theta)
vox= (40.0 m/s)(cos(35 degrees))
vox= (40.0)(0.8191)
vox= 32.76
vox= 32.8 m/s
In the y-direction:
voy= vosin(theta)
voy= (40.0 m/s)(sin(35 degrees))
voy= (40.0)(0.5735)
voy= 22.94
voy= 22.9 m/s
How much time passes until the projectile is at the top of its trajectory?
At the top of the trajectory the y-velocity of the projectile will be 0.0 m/s. The object is still moving at this moment, but its velocity is purely horizontal. At the top, for an instant, it has quit moving up and is about to start moving down. At that moment the projectile is not moving up nor down, only across.
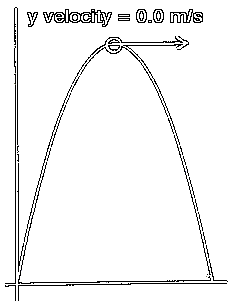
At the top:
| Two dimensional velocity: | Non-zero, aimed to the right |
| X-velocity: | Positive non-zero, equal to two dimensional velocity |
| Y-velocity: | 0.0 m/s |
In the diagram to the left, the vector shown at the top of the trajectory should be considered to be the two dimensional velocity vector. Note that at this moment the projectile is moving directly right, with no up nor down movement. The y-velocity at this point is 0.0 m/s.
We need to find out how much time passes from the time of the throw until the time when the y-velocity of the projectile becomes 0.0 m/s. This y-velocity at the top of the trajectory can be thought of as the final y-velocity for the projectile for the portion of its flight that starts at the throw and ends at the top of the trajectory.
We will call this amount of time 'the half time of flight', since the projectile will spend one half of its time of flight rising to the top of its trajectory. It will spend the second half of its time of flight moving downward.
General:
We can use the following kinematics equation:
vf= vo+ at
Subscript it for y:
vfy= voy+ ayt
Solve it for t:
t = (vfy- voy) / ay
Plug in 0.0 m/s for vfy:
t = (0.0 m/s - voy) / ay
If the original y-velocity and the y-acceleration (the acceleration due to gravity) are plugged into the above equation, it will solve for the amount of time that passes from the moment of release to the moment when the projectile is at the top of its flight.
Example:
Start with:
t = (vfy- voy) / ay
Plug in 0.0 m/s for vfy:
t = (0.0 m/s - voy) / ay
Plug in values for voy and ay:
t = (0.0 m/s - 22.9 m/s) / - 9.8 m/s2
t = -22.9 / -9.8
t = 2.33
t = 2.3 s
In this example 2.3s of time passes while the projectile is rising to the top of the trajectory.
How high does the projectile rise?
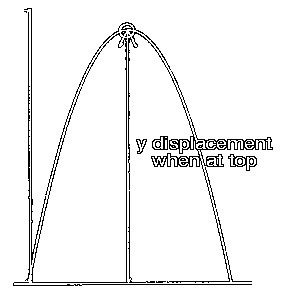
Here you need to find the displacement in the y-direction at the time when the projectile is at the top of its flight. We have just found the time at which the projectile is at the top of its flight. If we plug this time into a kinematics formula that will return the displacement, then we will know how high above ground the projectile is at when it is at the top of its trajectory.
General:
Here is the displacement formula:
d = vot + 0.5at2
We must think of this displacement in the y-direction, so we will subscript this formula for y:
dy= voyt + 0.5ayt2
If now we plug in the half time of flight, which was found above, we will solve for the height of the trajectory, since the projectile is at its maximum height at this time.
Example:
Starting with:
dy= voyt + 0.5ayt2
Then plugging in known values:
dy= (22.9 m/s)(2.33 s) + (0.5)(-9.8 m/s2)(2.33 s)2
dy= 53.35 - 26.60
dy= 26.75
dy= 27 m
How much time passes until the projectile strikes the ground?
General:
With no air resistance, the projectile will spend an equal amount of time rising to the top of its trajectory as it spends falling from the top to the ground. Since we have already found the half time of flight, we need only to double that value to get the total time of flight.
Example:
t = 2(2.33 s)
t = 4.66
t = 4.7 s
This is the total time of flight.
How far away does the projectile land from its starting point?
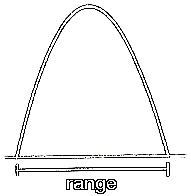
The distance from the starting point on the ground to the landing point on the ground is called the range of the trajectory. This range is a displacement in the x-direction. It is governed by the x-velocity of the projectile. This x-velocity does not change during the flight of the projectile. That is, whatever is the value of the x velocity at the start of the trajectory will be the value of the x-velocity throughout the flight of the projectile. The x-velocity remains constant because there are no accelerations in the x-direction. The only acceleration is in the y-direction, and this is due to the vertical pull of gravity. Gravity does not pull horizontally. Therefore, the calculation for the range is simplified.
General:
Let us start with the general displacement formula:
d = vot + 0.5at2
Since we are working in the x-direction, we should subscript this equation for x:
dx= voxt + 0.5axt2
Now, since the acceleration in the x-direction is 0.0 m/s2, the second term in the above equation drops out, and we are left with:
dx= voxt
The velocity in the x-direction does not change. The projectile maintains its original x-velocity throughout its entire flight. So, the original x-velocity is the only x-velocity the projectile will have. We could, therefore, think of the last equation as:
dx= vxt
If we plug in the original x-velocity for vx and the total time of flight for t, we will solve for the horizontal displacement, or range, of the trajectory.
Example:
As shown in the general section above, start with:
dx= vxt
Plug in values. Remember that the x-velocity is constant and always equal to its original value and that the time here is the total time of flight.
dx= (32.8 m/s)(4.66 s)
dx= 152.84
dx= 150 m