Work
Definition Of Work
Work is the transfer of energy.
In physics we say that work is done on an object when you transfer energy to that object.
If you put energy into an object, then you do work on that object (mass).
If a first object is the agent that gives energy to a second object, then the first object does work on the second object. The energy goes from the first object into the second object.
At first we will say that if an object is standing still, and you get it moving, then you have put energy into that object. The object has kinetic energy as a result of your work. You pushed it through a displacement, you did work on the object.
 For example, a golfer uses a club and gets a stationary golf ball moving when he or she hits
the ball. The club does work on the golf ball as it strikes the ball. Energy leaves the club and enters the ball.
This is a transfer of energy. Thus, we say that the club did work on the ball.
For example, a golfer uses a club and gets a stationary golf ball moving when he or she hits
the ball. The club does work on the golf ball as it strikes the ball. Energy leaves the club and enters the ball.
This is a transfer of energy. Thus, we say that the club did work on the ball.
And, before the ball was struck, the golfer did work on the club. The club was initially standing still, and the golfer got it moving when he or she swung the club.
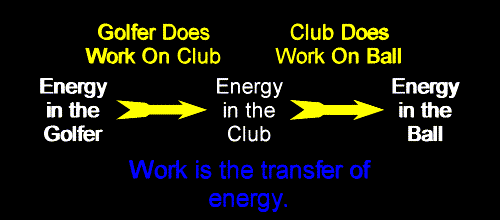
So, the golfer does work on the club, transferring energy into the club, making it move. The club does work on the ball, transferring energy into the ball, getting it moving.
Formula For Work
In almost all cases considered when studying mechanical forms of energy, when work is done on an object a force is applied to the object, and the object is displaced while this force is acting upon it. That is, the object moves as a result of a force being placed on it.
In the previous golf example the club places a force on the ball, and this force acts on the ball over the short distance through which the club and the ball are in contact as the ball is being hit. Energy is transferred as the force acts over this displacement.
The amount of work is calculated by multiplying the force times the displacement. That formula looks like this:
![]()
A word about dot products: On the right of the equal sign is the dot product of the force vector times the displacement vector. If the object is displaced in the same direction as the force is pushing, then this dot product becomes a simple multiplication of the size of the force times the size of the displacement.
At first we will consider only forces that are aimed in the same direction as the displacement. So, we will be using the simple multiplication mentioned above. For example, we will imagine an object being pushed horizontally to the right, and the object will be moving horizontally to the right as a result of this applied force.
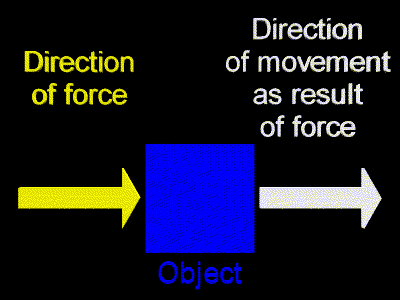
Below is an animation that shows just that. The force vector is drawn in blue. It is pushing the object to the right. This force is applied over a displacement. The displacement vector is shown in red. The yellow object (mass) starts out standing still. While the force is acting on the object the object picks up speed, that is, it accelerates. When the force quits acting, the object quits picking up speed; that is, it quits accelerating.
A medium force acts on the object (mass) over a medium displacement:
Notice that in the above animation the object picks up speed while the force is acting upon it. This picking up of speed means that the object is gaining more and more energy (kinetic energy) as the force is acting on it. While the force is acting upon the object, energy is being transferred to the object. Therefore work is being done on the object. Whatever we might imagine is providing the force is the agent that is doing work on the object. In our above discussion the force could be applied by the golf club, and the object in the animation represents the golf ball. This, of course, would need to be thought of as in slow motion!
Now, since work is calculated as the product of force times displacement, many different combinations of forces and displacements could yield the same work, or the same energy transfer. Using units of Joules (J) for work, Newtons (N) for force, and meters (m) for displacement:
W = (F)(d)
12 J = (1N)(12m)
12 J = (2N)(6m)
12 J = (3N)(4m)
So, small forces acting over large displacements can do the same work as large forces acting over small displacements.
For example, compared to the above animation, the following animation has a larger force that acts over a shorter displacement, yet the same amount of work is ultimately done.
A large force acts on the object (mass) over a small displacement:
And in this next animation, compared to the first, a smaller force and a larger displacement is demonstrated. Again, the same amount of work is done. The same amount of energy is transferred.
A small force acts on the object (mass) over a large displacement:
Later, we will see what happens when a force is applied at an angle to the displacement. For a while, though, we will consider only forces in the same direction as the displacement.
Sample Calculation
How much work is done if a force of 20 N is used to displace an object 3 m?
| W = F · d | Formula for work. |
| W = (20 N)(3 m) | Plug in values for force and displacement. |
| W = 60 N-m | Work equals 60 units of energy transferred. Looks like the unit for energy transferred, and thus, the unit for energy, is Newton-meter. However, it is usually not done that way. |
| W = 60 Joules | Energy units are called Joules, 1 Joule is equal to 1 Newton-meter. A Joule is the MKS metric unit for energy. |
| W = 60 J | Joule is abbreviated J. |
Questions
Here are some questions to work with using the above formula.