Net Force
Several forces can combine to make a total, or net, force.
More than one force can act on an object at once. For example, two people could push on a book at the same time. One person could push toward the left and the other could push toward the right. In this case the two forces would act against each other. If the force toward the left was greater than the force toward the right, then the prevailing force would be toward the left. The strength of this prevailing force would be the difference between the strengths of the two separate forces. This prevailing force is called the net force.
For example, if one person pushed the book with a force of 20 Newtons toward the left, and the other person pushed the book with a force of 18 Newtons toward the right, then that the net force would be 2 Newtons in size and directed toward the left. Here is a picture showing those forces:
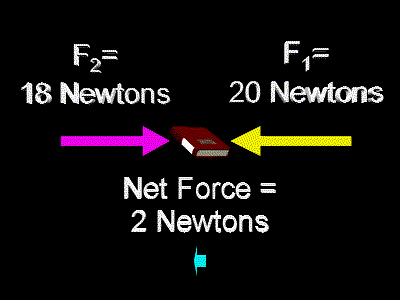
As you can see, the net force is aimed toward the left. This object will move as if it had a single force of 2 Newtons pushing on it toward the left.
Forces can be positive or negative.
Actually, forces which are aimed to the right are usually called positive forces. And forces which are aimed to the left are usually said to be in a negative direction. So, to be more accurate, in the above diagram we should call F1 a negative force, that is, negative 20 Newtons, and we should call F2 a positive force, or positive 18 Newtons. This is shown in the following diagram. Notice that the net force is aimed to the left; so, it is a negative force.
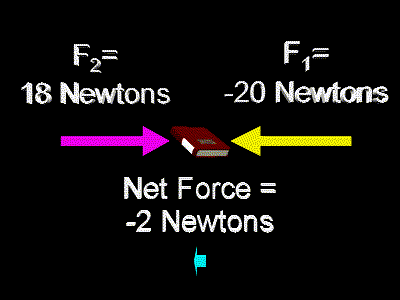
Basically, when you calculate the net force you add up the separate forces, as in:
F1 + F2 = (-20 N) + (18 N) = -2 N = Fnet
Two forces can cancel each other.
Now, perhaps the two people pushing on the book each push with the same strength, again one person pushing toward the left and the other pushing toward the right. In this case the two forces would exactly cancel each other out. The net force on the book would be 0 Newtons. Here is a picture of that situation:
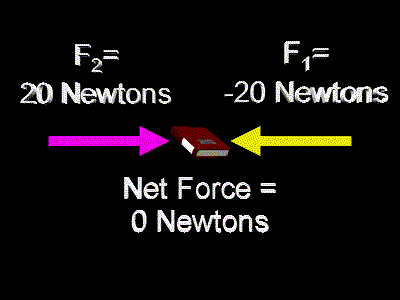
When two or more forces cancel each other out to create a net force of zero as in the above diagram, we say that the forces on the object are balanced. We also say under these conditions that the forces on the object are in equilibrium. Under such conditions it is as if there is no force on the object. The object will not accelerate. That is, the velocity of the object will not change.
Forces in the same direction work together.
Also, consider the two people to be pushing the book both in the same direction. If one person pushed to the right with a force of 8 Newtons, and the other person also pushed to the right with a force of 6 Newtons, then the net force on the book would be 14 Newtons toward the right. In this case the two forces would complement each other, rather than tending to cancel each other. Here is a picture of that:

This object will move as if it had a single force of 14 Newtons pushing on it toward the right.
Forces can act in directions other than horizontal.
The above three situations have all been one dimensional. When the only directions considered are to the left or to the right, then the problem can be thought of as operating on a horizontal number line, usually called the x-axis. Such situations occurring along one line are called one dimensional.
One dimensional problems may also be vertical. In our context here we might consider only forces that act up or down. That would be a one dimensional problem, also. It would be operating on a vertical number line, usually called the y-axis.
However, if several forces act upon one object they need not act only along one line. For example, an object could be pushed toward the right by one force and upward by another. In this case the net force would be neither simply horizontally toward the right nor simply vertically upward. It would be aimed in a slanted direction upward and to the right. Nor would the size of this net force simply be the arithmetic sum of the sizes of the two other forces. In this situation one would use vector mathematics to calculate the net force.