Non-inertial Frame of Reference 2

Below is an animation of a rotating disk. Near the edge of the disk is an (x, y, z) coordinate system which is, of course, following a curved path. This coordinate system is moving in circular motion. The speed of the coordinate system is constant; however, it is accelerating.

It is accelerating because its velocity is changing. Its velocity is changing because the direction of its movement is changing. Since velocity is made up of both speed and direction, when the direction changes, the velocity changes.

Since this coordinate system is accelerating, it is an example of a non-inertial frame of reference.

Non-inertial frames are accelerating frames.

• The Rotating (X, Y, Z)
• Non-inertial Frame
• Accelerating
• Velocity Is Not Constant

Since this is a non-inertial frame of reference, you should feel a fictitious force if you are using it as a reference. And you would. It would be especially noticeable if the disk were spinning quickly. You would feel pushed off of the disk. This force is often called the centrifugal force. It is a fictitious force. It really does not exist.

Actually, if you were near the edge of this disk, at any moment your velocity would be tangent to the circle in which you were moving. In the diagram below you would be like the blue dot which you could imagine moving in a circle.

Now, pretend this spinning is happening with you on a children's merry-go-round. Almost everyone has been on one of these. At the moment shown above, you are the blue dot, and your velocity is tangent to the circle. According to Newton's first law(which is mostly a restatement of the law of inertia) you should continue to travel in a straight line tangent to the circle. That is, you would try to maintain your velocity and move along the line tangent to the circle as shown in the next diagram:

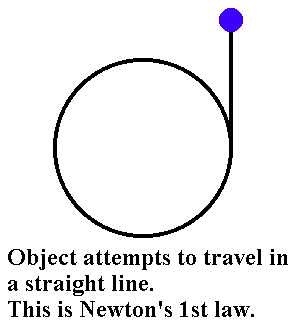
However, you will want, we will suppose, to stay on the merry-go-round. To do that you will have to 'hang on' by pulling yourself toward the center of the circle. Most likely you will grab on to the bars or posts mounted on the merry-go-round and pull yourself inward like the next diagram shows.

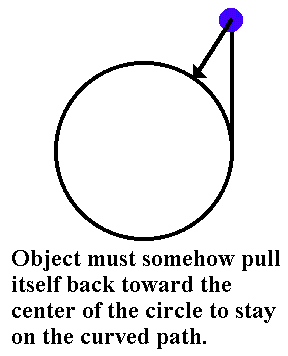
Very most likely, however, you will interpret the pull you provide toward the center as your attempt to resist somehow being 'pushed away' from the center of the circle. This outward, away from the center force does not really exist, however. You are not being 'pushed away' from the center. You are just trying to go in a straight line and must provide a center seeking force to make you go around the turn and stay on the merry-go-round.

The fictitious force away from the center of rotation is called the centrifugal force.

The force you apply, pulling yourself back in toward the center and keeping you on the merry-go-round is called the centripetal force.

Centrifugal force: Fictitious force imagined on an object in a rotating frame of reference. Incorrectly thought as pushing the object away from the center of its circular motion.

Centripetal force: Actual force which must be applied to an object in order to keep it moving in a circle.