Vectors - An Introduction

This may be the first time that you have encountered the concept of a vector. Vectors are central to the study of physics. Since they may be new to you, do not at first try to relate them to ideas that you already have. That may just confuse the issue.

It will take a short while to unravel this definition. You will end up understanding vectors to be items that have two parts.

Let us first be sure that we understand what is meant by the word quantity.

When we measure something, such as the time it takes you to read this paragraph, we can write down that measurement as a number usually followed by a unit. For example, it may take you 30 seconds to read this paragraph. Using the symbol t for time, one could write down:

t = 30 s

Usually, we would say, "The time period was 30 seconds long." Or we might say, "30 seconds passed." For now, though, let us say that the quantity of time has a size of 30 seconds.

In the above example the time period can be completely explained and expressed using only one number, 30 seconds. That number represents the size of the time, and, as a quantity, all that time has is a size. Another quantity that only has a size is the temperature of the room in which you are located. We might say that the temperature is 72 degrees Fahrenheit. The quantity of mass, also, only has a size. We could say, "The mass of the book is 1.2 kilograms." We would be completely stating that quantity of mass with only one number, 1.2 kilograms.

Quantities like these, that only have size, are called scalars.

Not all quantities are like this. Some have more than size; some also have a direction. Quantities with both a size and a direction are called vectors.

Let us take a look at the concept of velocity as it is used in physics. Velocity can be measured. It is a quantity that can be written down. However, in the study of physics we would say the the following statement does not completely explain nor express a velocity:

v = 25 m/s

The above statement would read, "The velocity equals 25 meters per second." The size of the velocity would be 25 meters per second. That, though, is not enough. It turns out that velocities have more that just a size. They also have a direction. For example, a statement correctly states a velocity would say, "The velocity equals 25 meters per second North ." Notice that two things are necessary to state a velocity, as size, that is, 25 meters per second, and a direction, North. Now this is how you talk about velocities when you are studying physics. The size of the velocity is actually called the speed. So, we would say that velocity is made up of a speed and a direction.

Quantities like this, that have sizes and directions, are called vectors.

When we say that a quantity has a direction, we mean a direction much like how a direction is thought about on a compass. The velocity of a thrown baseball, of course, is pointed or aimed in the direction that the ball is moving. That is not how we are speaking about direction when we say, "Time marches forward," nor when we say, "The temperature is going up." Time nor temperature are not aimed North, South, East, nor West, or any other compass direction.

Well, it should not be too difficult to understand that the size of the velocity, that is, 25 meters per second, is a number. The direction, also, is described with a number. In the above discussion we stated the direction as North. Almost always directions are a bit more complicated that that. Usually directions are stated using language such as...

The direction is 40 degrees North of East.

So, a complete vector description of velocity could be written as...

The velocity is 38 m/s in a direction of 52 degrees West of North.

This 'North of East' and 'West of North' language can be a little confusing at first. More about that in a moment. For now it is important to understand that a vector has two parts; one part is the size, and the other part is the direction. Both parts can be expressed with numbers.

There is a way to draw vectors. They are drawn, or symbolized, if you like, with arrows. An arrow is a perfect symbol for a vector. An arrow has a size, its length, and a direction, the direction in which it is pointing. So, to draw a vector we need just to draw an arrow:

After clicking on the above buttons a few times, you should be able to realize that an arrow could be of any size and point in any direction. It could, therefore, represent the velocity of a person on a bicycle moving at any speed, traveling in any direction.

The length of the arrow is the size of the arrow. It is the length of the arrow that represents the size of the vector. If we are talking about a velocity vector, then the length of the arrow represents the size of the velocity. The size of the velocity is usually called the speed.

The direction that the arrow is pointing represents the direction of the vector. For a velocity vector used to describe the motion of an object, it would represent the direction in which the object was moving.

The tip of the arrow, that is, its point, is called the head of the vector. The other end of the arrow is called the tail of the vector.

Now, if you have any confusion concerning the 'North of East' language used above to describe the direction of a vector, let us clear that up now.

First of all, imagine an x, y coordinate system. Imagine that the positive y direction, which is pointed up, is North and that the negative y direction, downward, is South. Imagine that to the right, or positive x direction, is East, and that to the left, or negative x direction is West. Just imagine that the axes are labeled that way. These labels really do not necessarily have anything to do with any true compass directions. So, picture in your mind a coordinate system like this:

       N
       |
       |
W -----+----- E
       |
       |
       S

Imagine the tail of the vector at the origin of this coordinate system. If the vector lies directly along one of the axes, then it is said to point directly North, South, East, or West, obviously according to what exact direction the vector is pointing. If, though, it lies between two of the axes, which will almost always be the case, its direction is stated using the two axes between which it lies. For example, a vector pointing toward the right, rising a bit above the x axes would be mostly aimed East, but raised toward the North. It would look like this:

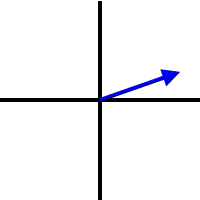
We would say this vector is directed a few degrees North of East. You could also think of it as pointing upward, but pushed quite a bit to the right. In that case it would be directed several degrees East of North. It is aimed North, but pushed toward the East.

All of this is easier seen than described. Try playing with the following active diagram. The color of the arc matches the color of the description for the direction. Just about every direction can be described in two ways. One not better than the other.

If a quantity has only a size, it is called a scalar. Time and temperature are examples of scalars. Mass, too, is an example of a scalar.

If a quantity has a size and a direction, it is called a vector and can be symbolized, or drawn, as an arrow. Velocity is an example of a vector.

Technically, speed just has a size. It is the size of a velocity. Speed is a scalar. We might say, "The object traveled at a speed of 8 meters per second." Notice that we do not know in which direction it was moving.

Velocity, since it is a vector, has a size and a direction. So, a velocity is made up of a speed and a direction. We might say, "The object is moving at a speed of 7 meters per second in a direction of 30 degrees South of East."

This may seem a little confusing at first, since often in casual speech speed and velocity are used interchangeably. However, in a physics discussion it is important to know this distinction and to be aware of its application.

Often the word rate is used to mean speed or velocity. Perhaps that's not a good idea. It's vague and begs the question, 'The rate of what?'

Distance is a scalar. It only has a size. It is the size of a displacement. We might say, "The distance traveled by the object was 45 meters." Notice that we do not know the direction in which the object moved.

Displacement is a vector with size and direction. We might say, "The object experienced a displacement of 30 meters in a direction 50 degrees South of West." We know how far the object moved and in what direction it moved.

Vectors are central to the study of physics. Early on in this study you will encounter types of vector quantities. Besides displacement and velocity, other examples of vectors include acceleration, force, gravitational field, torque, and electric and magnetic fields.