Two Source Interference Pattern 2D

Here is an interactive animation which shows the patterns that are produced when two circular periodic waves interfere. This is often termed a two source interference pattern. Explanations follow.

Source: 1 2

Same phase

Wavelength: S M L

Basic operation:

• The 'S', 'M', and 'L' (small, medium, large) radio buttons control the size of the waves.
• The 'Switch phase' button controls the phase of the sources. Directly to its right is a label that describes the current phase of the sources. The demo starts out with the sources in phase. This means that both sources emit a crest at the same time and a trough at the same time. When the sources are out of phase, as one creates a crest the other creates a trough.
• You can click and drag either source to a new location in the medium. When you click your mouse down, you will 'grab' whatever source is closest to the mouse. On a touch surface, the source will locate where you tap.
• The 'Initialize' button sets all parameters back to their original values.

 

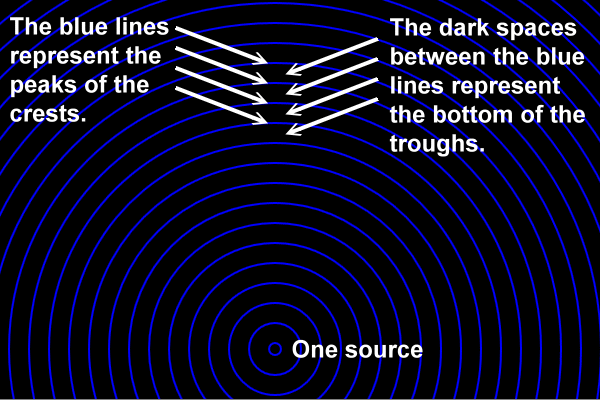
The blue, circular arcs represent the crests of the waves coming from each source. The space between the blue lines represent the troughs of these waves. Here's a diagram (with only one source turned on) that shows these crests and troughs:

 

Here, we are interested in a type of pattern that appears when we turn on both sources. Both sources emit a periodic wave of the same frequency, each emit from separate a location. We are interested in a stationary (non-moving) pattern of wave cancelation that appears when the waves from one source interfere with the waves from the other source. This pattern, this shape, is called an interference pattern.

 

At first, we are going to discuss the situation where the two sources of waves are in phase. This means that the two sources have the same frequency and when one emits a crest, the other emits a crest. So, as you use this page's animated interference demo, be sure to have the sources in phase so that you correctly relate to the following diagrams.

 

Although these waves are not necessarily examples of water waves, it is easy and meaningful to think of them that way. Imagine that you are near the edge of a calm pond, tapping the water rhythmically with two sticks. The two spots where your sticks tap the water represent the two sources.

 

Although both sources are repeatedly producing waves (disturbances) which move across the medium, at certain locations the medium is motionless. These motionless locations are caused because the wave from one source destructively interferes with the wave from the other source.

 

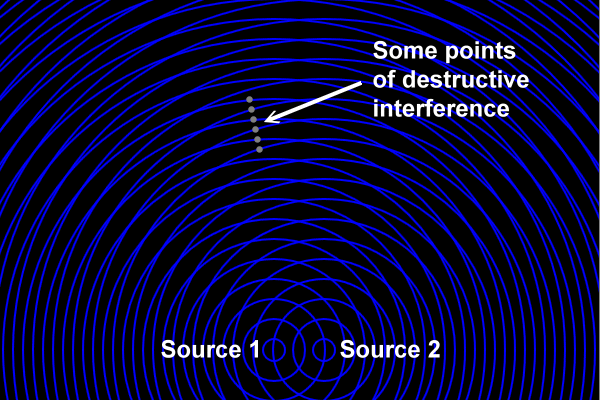
Here's a magnified view of the above region:

 

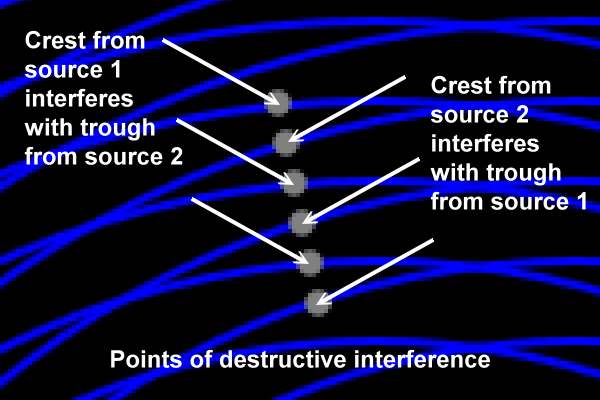
These destructive interference points form a shape, or pattern. These patterns look like straight lines, but they are actually shaped like hyperbolas.

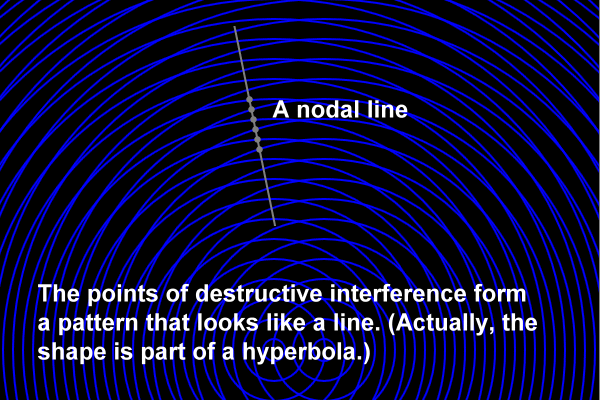
These points of destructive interference are often called nodal points:

 

These nodal points line up to form a nodal line (actually, it is a rather straight looking part of a hyperbola):

 

The interference pattern has several nodal lines. They are numbered from the center outward on each side of the diagram, starting with 1:

 

How many nodal lines appear depends on the wavelength of the waves and the distance between the sources. Here is a diagram with shorter wavelengths than before. Note the numbering of the nodal lines:

 

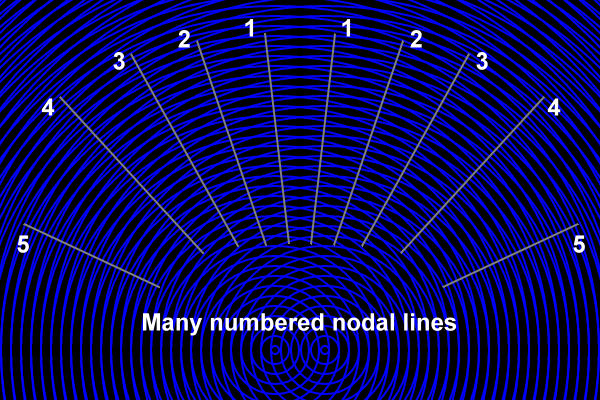
What is interesting about the nodal lines is that they do not move. The waves, the blue lines, are moving. However, there are these locations called nodal lines where the two waves from the two sources always cancel, always destructively interfere. These nodal line locations do not move. Run the demo at the top of this page. Notice that the waves move, but the nodal lines do not.

If these waves were ripples on water, then the nodal lines would be places where the water was still, where the water was not rippling. If you were in a small boat, you could safely paddle along a nodal line while large waves rippled up and down to your right and left. The water along the nodal line would be calm.

If these waves were sound waves, then there would be silence along a nodal line. You could walk down a nodal line and hear nothing. But you would hear the sound waves if you ventured off of your nodal line.

If these waves were light waves, then it would be dark along the nodal lines. You would have to imagine yourself very tiny to fit in a diagram where the wavelength of light was represented by the distance between the blue arcs. If you could, though, be on a nodal line and look toward the sources of light, you would not see any light coming from them. If you moved off of the nodal line, then you would see them shining. (There is no medium for light waves, but they do interfere this way.)

 

Basically, nodal lines and nodal points are stationary places where the medium does not vibrate because waves from two (or more) sources completely  and continuously destructively interfere there. The waves move, but the spots where they cancel do not move. Since the nodal lines do not move, they are easy to see and measure.

 

Why are these nodal lines important?

• If you can set up an interference pattern like this one, measuring the positions of the nodal lines along with the distance between the sources allows you to determine the wavelength of the waves causing the pattern.
• The nodal line interference pattern proves that the sources are emitting waves. In fact, the wave nature of light was first shown by setting up just such an interference pattern as this.

 

And then there are the anti-nodal lines. There are also stationary places within this interference pattern where a crest always meets a crest and where a trough always meets a trough. These are places where there is always constructive interference. These places are called anti-nodal lines. They look quite like straight lines, but are again sections of hyperbolas. Here's some points in the pattern where constructive interference always occurs:

 

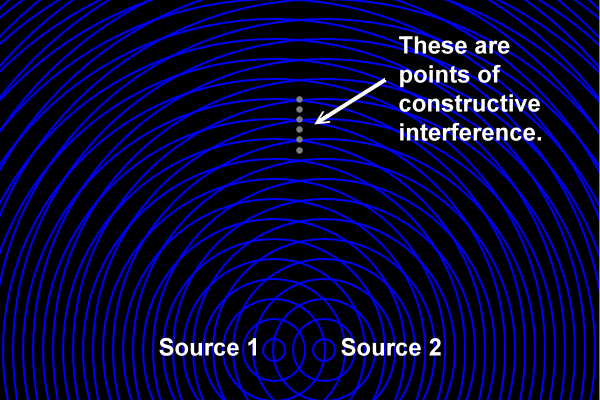
Here is an enlarged view. Note that at an anti-nodal point crest meets crest and trough meets trough.

 

The anti-nodal points form anti-nodal lines. There are several anti-nodal lines in our interference pattern as shown in the following picture:

 

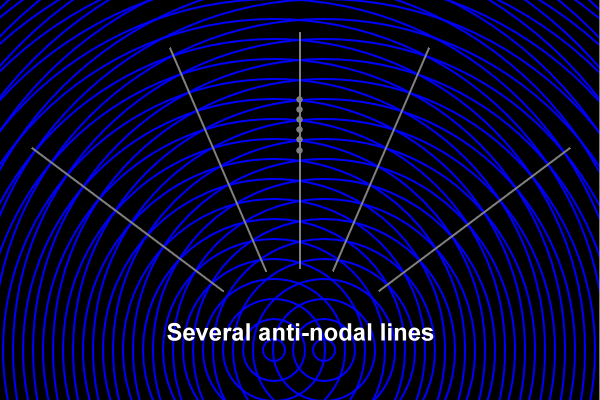
If these were water waves, and you were on an anti-nodal line in a small boat, then the sea would be very active. The water would go way up when crest met crest and way down as trough met trough.

If these were sound waves, you would hear a loud sound while standing in an anti-nodal line.

If these were light waves, you would see the sources shining brightly from you location on an anti-nodal line.

 

Be sure to take a look at the Two Source Interference Pattern in 3D demonstration page. In this demo the amplitudes of the two interfering waves are added, and the result is shown as a height or depth on a mesh surface. You can clearly see the stationary nature of the nodal lines: