EZ Graph - Vertical Hyperbola
A vertical hyperbola drawn on the (x, y) plane has one section that opens upward and another section that opens downward. This is the equation for a vertical hyperbola:
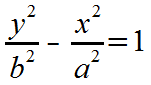
Here is our EZ Graph graphic calculator preloaded with two functions that are based on the above equation (click 'Draw graph'):
The algebra for getting to 'y = ':
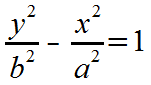 |
The starting equation |
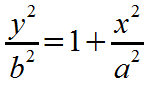 |
Add x2/a2 to both sides. |
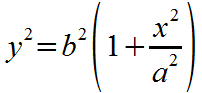 |
Multiply both sides by b2. |
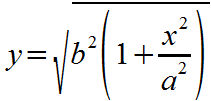 |
Take the square root of both sides. Solve for the positive square root. |
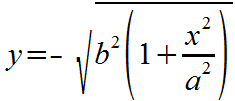 |
And solve for the negative square root. |
Now, the above two equations that start with 'y =' must be translated into math statements that EZ Graph understands:
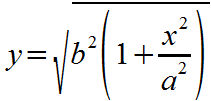
 f1(x) = sqrt(b^2 * (1 + (x^2/a^2)))
f1(x) = sqrt(b^2 * (1 + (x^2/a^2)))
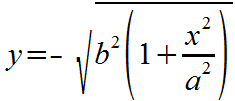
 f2(x) = -sqrt(b^2 * (1 + (x^2/a^2)))
f2(x) = -sqrt(b^2 * (1 + (x^2/a^2)))
We have what we need to graph the hyperbola: two equations, or functions of x. The first (with the positive square root) will draw the top part of the hyperbola, and the second (with the negative square root) will draw the bottom part of the hyperbola. Note that these are the two functions entered into EZ Graph for f1(x) and f2(x). If you remove the check next to one of these functions, that function will not be drawn, and you will see only half of the hyperbola.
Related:
Simple Rational Function f(x) = 1/x