The Bouncing 3D Cube

This animation shows a cube moving about a three dimensional space. It presents two dimensional projections of this motion into several planes. Please see notes below.

The purpose of this animation is to visualize several slices or projections of three dimensional projectile motion. These projections show that the object accelerates only in the planes that are aligned with the pull of gravity. This acceleration is seen in the common parabolic trajectory of projectile motion. In the plane perpendicular to the pull of gravity we see no acceleration as evidenced by the straight line motion projected into that plane. Please continue reading for more explanation.

First, the xyz axes: The xyz axes form a three dimensional coordinate system that has three axes: the x-axis, the y-axis, and the z-axis.

When you first load this page and before you make any changes to the animation....

• The x-axis is the red horizontal line. It runs from -60 on the left to +60 on the right.
• The y-axis is the green vertical line. It runs from -60 on the bottom to +60 at the top.
• The z-axis is the blue line that you are looking straight down. It looks like a blue dot because you can not see its length. You will need to rotate the xyz axes to see its length. Imagine this axis as coming out of and going into the screen. It runs from -60 behind the screen to +60 in front of the screen.

The spinning buttons: The animation can be spun in various ways with the 'Theta' and 'Phi' buttons. Theta and phi are two angles that control two rotations of the entire xyz axes. Each rotation can go in two directions, and these two directions are controlled by the two buttons near the 'Theta' and 'Phi' labels. After a fresh load of this page click the left 'Theta' button once, then click the left 'Phi' button once, and you will get a clear view of all three axes:

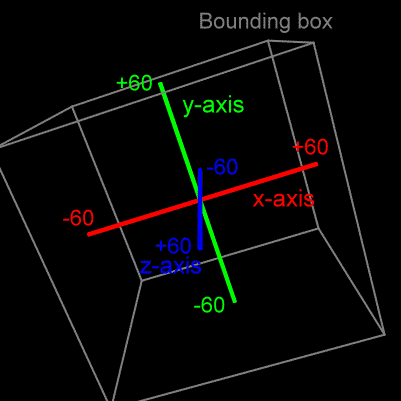
Also note the gray bounding box. The center of the bouncing cube stays within these bounds.

Two other buttons: The 'Rho' buttons move the xyz axes closer to or farther from you. The 'Reset' button gets you back to the original fresh page load view of the xyz axis.

What you can see: The middle column of checkboxes control the visibility of several aspects of the animation. More about these a bit further down the page; however, basically:

• The 'Cube' checkbox shows or hides the bouncing cube.
• The 'XY Plane', 'XZ Plane', and 'YZ Plane' checkboxes show or hide their respective planes.
• The 'XY Shadow', 'XZ Shadow', and 'YZ Shadow' checkboxes show or hide the projection of the cube's motion onto their respective planes.

About the planes and shadows: This animation shows motion in a three dimensional space. It is interesting to see two dimensional slices of this three dimensional space and to see projections or shadows of the three dimensional motion into or upon these two dimensional slices or planes.

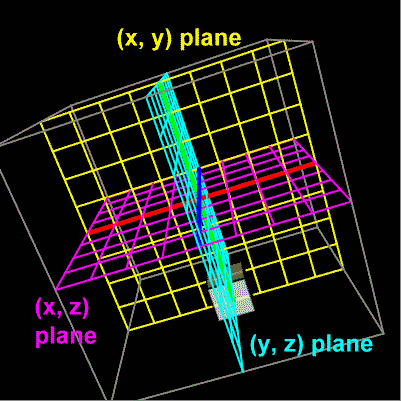
This animation lets you see three slices of the (x, y, z) space. It lets you see the (x, y) plane, the (x, z) plane, and the (y, z) plane. There are checkboxes that let you see or hide these. Checkboxes labeled as 'shadows' show or hide an image within the corresponding plane that follows the cube, but with just two dimensions shown, rather than three.

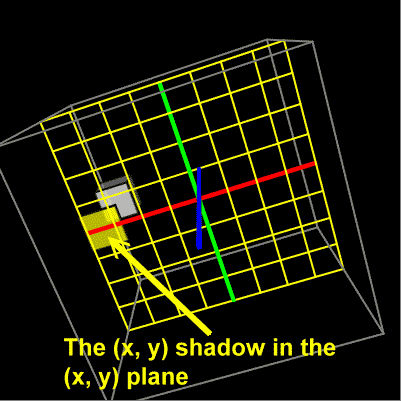
Hopefully, this animation helps you see how just a part of the motion can be examined while other parts of the motion are temporarily ignored. It's often handy to see a three dimensional motion considering only two of the axes. If you activate the (x, y) plane and the (x, y) shadow, for example, then you will see the projection of the cube on to the (x, y) plane. It will look pretty much like a flat square moving around.

About the acceleration buttons: You can consider these to control the direction in which gravity pulls.

The central ideas to this animation: The cube is moving with projectile motion in a three dimensional space. The acceleration due to gravity can be 'turned on' in any of six directions, or it can be completely 'turned off'.

The acceleration makes the path, or trajectory, of the cube to be curved. It's trajectory is a parabola. This curved path, however, is only mapped out, or shadowed, in the planes that contain the axis along which gravity is pulling.

Within the plane that does not contain the acceleration axis, or direction, the motion is not curved. No parabola there. It's straight line motion.

For example, at startup the acceleration due to gravity is aimed in the negative y-direction. We often liken this to 'downward' in most diagrams. The cube bounces around in a curved three dimensional path. But if you click on the (x, z) plane and shadow, and spin things around a bit so that you are looking directly into this plane, you will see that this slice of the motion shows up as straight line motion because there is no acceleration active in either the x- or z-direction. The acceleration is along the y-axis.

Well, there are two other planes to look at. If you examine the motion of the shadow in both the (x, y) and (y, z) planes you will see that the shadow is moving along a parabola, a curved path. This is because the acceleration is along the y-axis, and the y-axis is within these planes.

Try making the gravity work 'sideways' or 'up', and see if you can reason in which planes the motion will be straight lined or curved. Turn on any combination of planes and shadows to the several projections of this motion.

Try turning gravity 'off'. You should see straight line motions for all of the projections since there would be zero net force on the cube.