Direct Proportion

Direct Proportion Animation

The heights of these two bars vary in direct proportion to one another.

When one gets large, the other gets large; when one gets small, the other gets small - but this is happening in a special way.

When the blue bar grows so that it doubles (times 2) it size, the green bar also doubles (times 2) its size.

If the green bar shrinks so that its height is cut to one third (times 1/3), then the blue bar also shrinks to one third (times 1/3) its height.

The height of both bars change by the same factor.

Further explanations follow.

Quantities change.

When a quantity gets larger or smaller, we say that it changes.

Changes can be related through factor changes.

Sometimes a change in one quantity causes a change, or is linked to a change, in another quantity. If these changes are related through equal factors, then the quantities are said to be in direct proportion. Or one would say that the two quantities are directly proportional.

Twice the soup costs twice the money.

For example, suppose that you are buying cans of soup at the store. Let us imagine that they cost 50 cents, or $0.50, each.

Case #1:

Suppose that you buy 4 cans. You would pay $2.00.

Case #2:

Suppose that you buy 8 cans. You would pay $4.00.

So, changing the number of cans that you buy will change the amount of money that you pay.

Notice that the number of cans changed by a factor of 2, since 4 cans times 2 is 8 cans.

Also, notice that the amount of money that you must pay also changed by a factor of 2, since $2.00 times 2 is $4.00.

Both the number of cans and the cost changed by the same factor, 2.

Definition of Direct Proportion

When quantities are related this way we say that they are in direct proportion. That is, when two quantities both change by the same factor, they are in direct proportion.

In the above example the number of soup cans is in direct proportion to the cost of the soup cans. The number of soup cans is directly proportional to the cost of the soup cans.

The formal definition of direct proportion:

Two quantities, A and B, are in direct proportion if by whatever factor A changes, B changes by the same factor.

Half the volume of a liquid has half the weight.

Let us present another example of a direct proportion. The weight of a liquid is directly proportional to its volume.

Suppose that you had a container holding 6 quarts of a liquid, and that liquid weighed 3 pounds. If we poured out half of the liquid so that only 3 quarts remained, that liquid would now weigh 1.5 pounds.

So, the volume of the liquid changed by a factor of 1/2, since it went from 6 to 3 quarts, and since 6 quarts times 1/2 equals 3 quarts. The weight of the liquid also changed by a factor of 1/2 since it went from 3 to 1.5 pounds, and since 3 pounds times 1/2 equals 1.5 pounds.

Both the volume and the weight changed by the same factor, 1/2. So, in this example the weight and volume of the liquid are in direct proportion.

Symbol for directly proportional is alpha.

Here is a shorthand way to say that the quantities A and B are directly proportional:

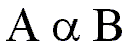The Greek letter between the A and the B is called alpha. It is here written in lower case script. In this context it is shorthand for the phrase 'is directly proportional to.' So, the above statement reads 'A is directly proportional to B.'

The form of the equation for a direct proportion looks like y = mx.

Whenever you have a direct proportion as stated above you can change it into an equation by using a proportionality constant. Here is how the direct proportion would look as an equation:

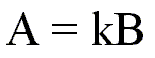The above would read 'A equals k times B.' The quantity k is a proportionality constant. If two quantities, A and B, are directly proportional, then there is a proportionality constant, k, such that k times B will equal A.

Note that the above equation has the same form as y = mx, a simple linear equation from mathematics that graphs a straight line through the origin with a slope of m.

The graph of a direct proportion is a straight line through the origin.

If A=kB, then a graph of A vs. B will yield a straight line through the origin with k as the slope:

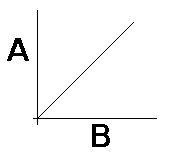straight line graph through origin, A vs. B

So, if you graph data for two related quantities, and that graph yields a straight line through the origin, then you know that the two quantities are in direct proportion.

Note again the similarity to the equation y = mx, where a line passes through the origin at a slope of m.

Examples of direct proportions abound in physics. For example, Newton's second law of motion states that the acceleration of an object is in direct proportion to the force on the object. So, if you triple the force on an object, then the acceleration of that object will also triple. Of course, when you triple a quantity you are changing it by a factor of 3.