Factor Change
When a quantity gets larger or smaller, we say that it changes.
For example, the volume of a certain liquid in a container can change from 3 quarts to 12 quarts. One could simply imagine extra liquid being poured into the container taking the volume from 3 quarts to 12 quarts.
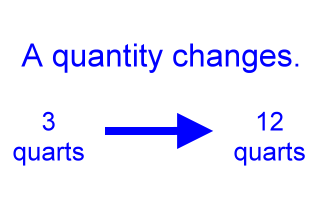
Factor changes are not additions or subtractions.
We can talk about this change in volume in several ways. One way is to say that 9 quarts were added, since 3 quarts plus 9 quarts is equal to 12 quarts. Talking about the change this way, however, is not talking about it in terms of a factor change. This is talking about the change as an additive change, not a factor change.

Factor changes are multiplications.
To understand factor change, think about it this way: 3 times 4 equals 12. So, times 4 is the multiplier that changes the 3 quarts into 12 quarts. We say, therefore, that the volume changed by a factor of 4.
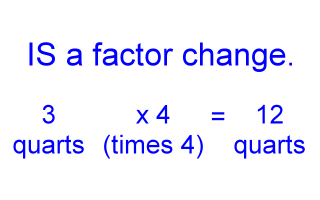
As we shall see next, the above mathematics shows a factor change of 4.
Factor changes are always discussed in terms of the multiplier that takes you from the initial quantity to the final, or changed, quantity.
A factor change of three (3):
If a distance changed from 5 meters to 15 meters, we would say that there was a factor change of 3 in the distance, since 5 times 3 is 15. We could also say, 'The distance changed by a factor of 3'.
A factor change of one half (1/2):
If a speed changed from 40 m/s to 20 m/s, we would say that the speed changed by a factor of 1/2. This is because 40 times 1/2 equals 20.
Again, the factor change in a quantity is the multiplier that takes you from the initial value of some quantity to the final, or changed, value of that quantity.
Here are some more examples, read across:
| Initial Quantity | Final Quantity | Factor Change | Since |
| 3 m | 30 m | 10 | (3 m)(10) = 30 m |
| 40 s | 10 s | 1/4 or 0.25 | (40 s)(1/4) = 10 s |
| 4.6 m/s | 12.8 m/s | 12.8/4.6 or about 2.78 | (4.6 m/s)(12.8/4.6) = 12.8 m/s |
| 5.3 kg | 1.1 kg | 1.1/5.3 or about 0.21 | (5.3 kg)(1.1/5.3) = 1.1 kg |
Notice that the factor change in a quantity can easily be calculated by taking the final quantity and dividing it by the initial quantity. For example:
- If a quantity starts out with a value of 7.2 (initially)
- And that quantity changes to a value of 9.6 (finally)
- Then the factor change is (9.6 / 7.2), or about 1.3
- Because 7.2 times (9.6 / 7.2) equals 9.6
Proportions can be defined in terms of factor changes.
Factor changes are important to understand when discussing proportions. Here is some related material: