Component style:
Fpara = 0
Fperp = 0
Required understanding
Changing the angle of the incline, theta
Let's take a closer look at the angle of the incline, and how changing it effects the sizes and directions of the weight components. In the demonstration below you can change the angle of the incline using the number adjuster labeled T. (T stands for 'theta'.) The incline and the vectors will be redrawn at the selected angle.
Thinking about the parallel force, notice that for small angles of incline, say 10 degrees, this force is small. At this angle the blue vector, Fpara, is short. For such a shallow incline there is only a small component of the weight that pulls the object down the incline. This makes common sense; things do not readily slide across floors that are only slightly slanted.
At a much larger angle of incline, say 80 degrees, the parallel force is much larger, the blue vector is long. For such a steep incline there is a large component of the weight that pulls the object down the incline. Again, this makes common sense. Most things would rapidly slide across a floor that was slanted almost vertically steep.
Mathematics for the parallel force
Can we see all of this in the formula for Fpara? That formula is:
The weight of the object, Fg, does not change when theta changes. The object's mass stays the same, and we stay on the same planet, so the weight stays constant. It is the value for the sine of theta that changes when theta changes.
In this section and the next we are going to talk about small and large numbers. Here we mean relatively small or large. For example, a value for the sine function over the angles we will be discussing can run between 0.0 and 1.0. So a number such as 0.17 will be considered small over this range, and 0.98 will be considered large. The cosine function values operate over the same range. The angles we are working with extend from 0 to 90 degrees; so over that domain we will call 10 degrees small and 80 degrees large.
Here's a graph of the sine of theta verses theta. The angle theta runs from 0 to 90 degrees; these are the possible sizes for the angle of incline. Over this domain note that the sine of a small angle equals a small value, and the sine of a large angle equals a large value.
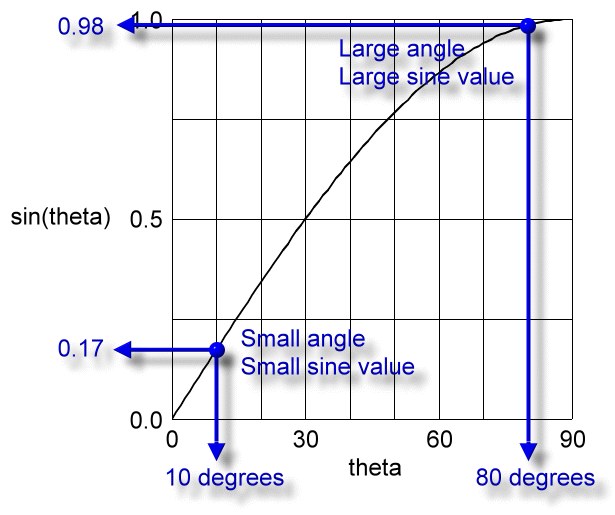
So from 0 to 90 degrees, if theta is small, the sine of theta is small, and we have this small number times the weight, so we get a small Fpara, and the object is pulled down the shallow ramp only a little. That's how it really works, correct? Objects do not readily slide down shallow inclines because there is not much of an Fpara to get them moving.
Small theta:

If theta is large, the sine of theta is large, so that's a large number times the weight, that creates a large Fpara, and the object is pulled down the ramp quite a bit. Objects tend to slide down steep inclines because of the large Fpara.
Large theta:

Mathematics for the perpendicular force
Let's look at the perpendicular force, Fperp, in much the same way as we did for the parallel force. The formula for the perpendicular force is:
Again, the weight of the object, Fg, does not change as theta changes. The value of the cosine function does change, though, as theta changes. Here's a graph of the cosine function from 0 to 90 degrees:
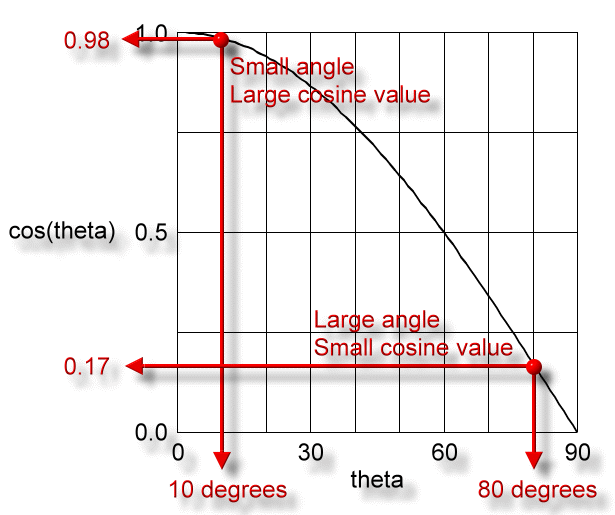
Now for angles between 0 and 90 degrees, if the angle is small, the cosine value for it will be large; if the angle is large the cosine value for it will be small.
So for a small angle the cosine value will be large, and we will have this large number multiplied by the weight to get a large perpendicular force. This makes complete sense; if the angle is small, the incline is close to flat, and most of the weight is directed perpendicularly into the surface.
Small theta:

For a large angle the cosine value is small. Multiplying it times the weight yields a small perpendicular force. Of course, if the incline is very steep, not much of the weight will be pressing into the surface.
Large theta:

Another way to see the components
In the above demo be sure to note the 'Component style' radio buttons. Switching between the two options shows you the two popular ways to draw the components of the weight vector. The difference is how the Fpara vector is drawn. It can be drawn from the center of the object, or it can be drawn positioned to form a right triangle with the other two vectors.
Related links