Introduction to the Inclined Plane
The inclined plane is a slanted surface, or ramp.
First, the non-inclined plane:
In the picture below we have a wooden surface with a gray object placed upon it. You can think of this wooden surface as the 'plane' in the term 'inclined plane'. However, this surface is not slanted, it is not inclined. It is flat with the ground. We will call this a flat surface. It has zero degrees incline.

Now, the inclined plane:
The picture below shows the same wooden surface, but now it is slanted, now it is inclined. In this picture the surface has an incline of twenty degrees. That means that there is a twenty degree angle between the flat horizontal ground and wooden surface.

In the above picture you might imagine that the object could slide down the incline. If there is only a small amount of friction between the object and the wooden surface, this could certainly be the case.
The frictionless inclined plane:
Here, at first, we will consider inclined planes with no friction. So, at first, our objects will be thought of as sliding down frictionless inclined planes.
The frictionless inclined
plane.
The object accelerates (moves faster and faster) as it slides
down the incline.

Required understanding for the inclined plane:
To understand the physics and mathematics of the inclined plane you will need to understand vectors, forces, and right triangle trigonometry (SOH-CAH-TOA). Here are some links within Zona Land Education that cover those topics:
Going on:
When you are done with the material on this page you may want to continue with the following sections. These links are repeated at the bottom of this page.
Inclined planes come in many shapes and sizes.
Inclined planes can be steep or shallow, and can be slanted to the right or the left.
The inclined plane is a simple machine.

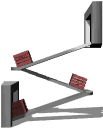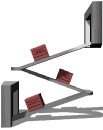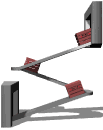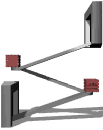
In physics there are several mechanisms called simple machines. The inclined plane is one of these.
Basically, a simple machine can give you a force advantage when you are moving something, often lifting something. A job that requires a lot of force can be made to require much less force if a simple machine is applied to the problem.
An inclined plane when used as a ramp is a simple machine because it takes less force to push an object up the ramp than to lift it vertically straight up. So a person who is not strong enough to lift a box up to a higher level could be able to push it up a long shallow ramp to the higher location, especially if the box had wheels to keep the friction low. The ramp allows the job of raising the box to be done with less force than the weight of the box.
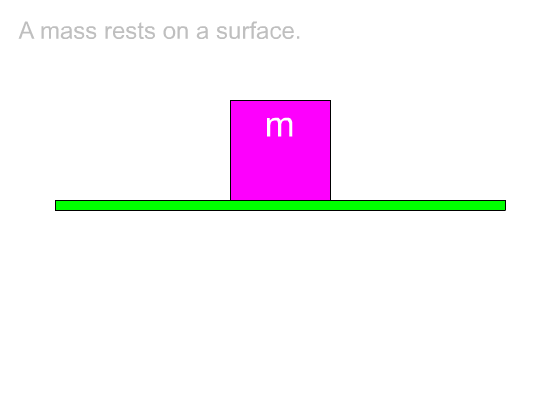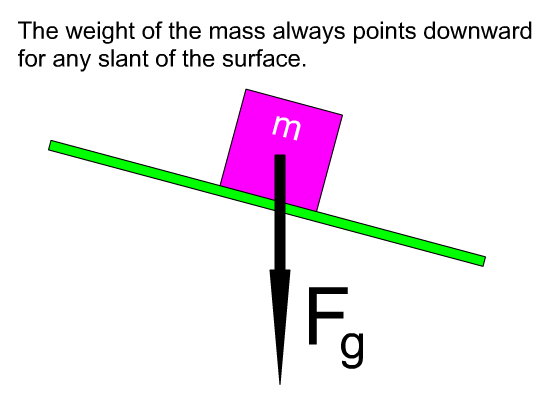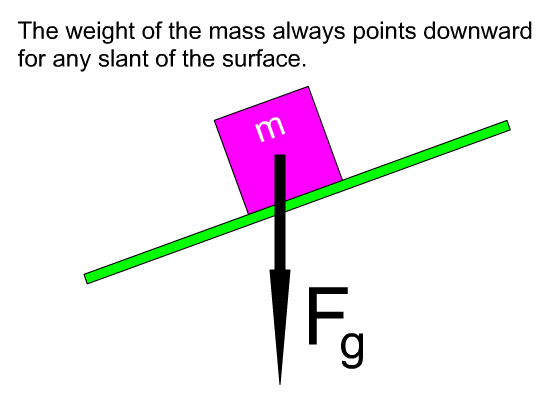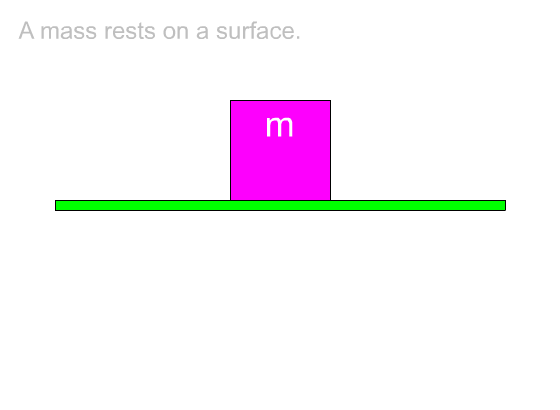
The weight of an object always points downward.
The weight of an object points toward the center of the Earth. That direction does not change if the slant of the incline changes.
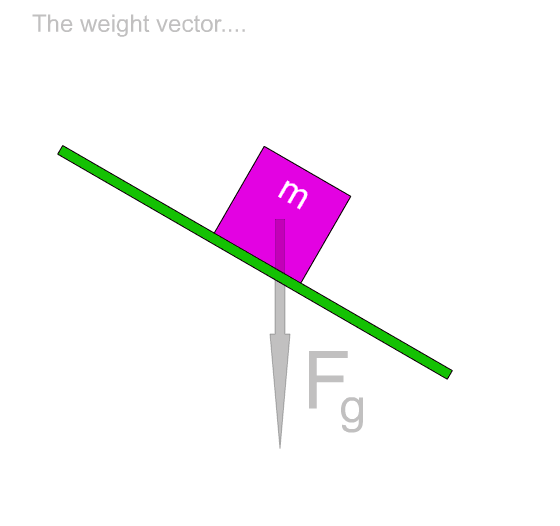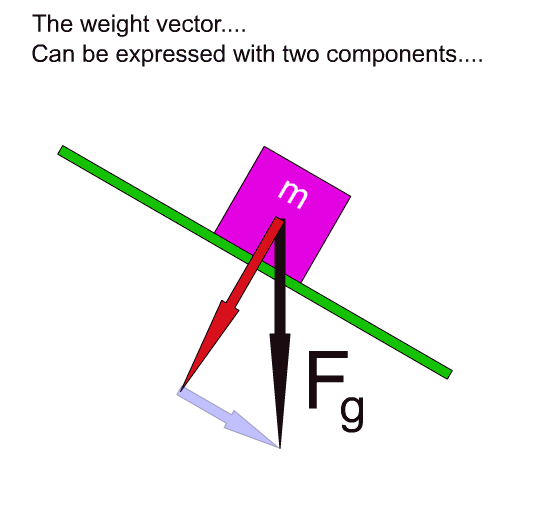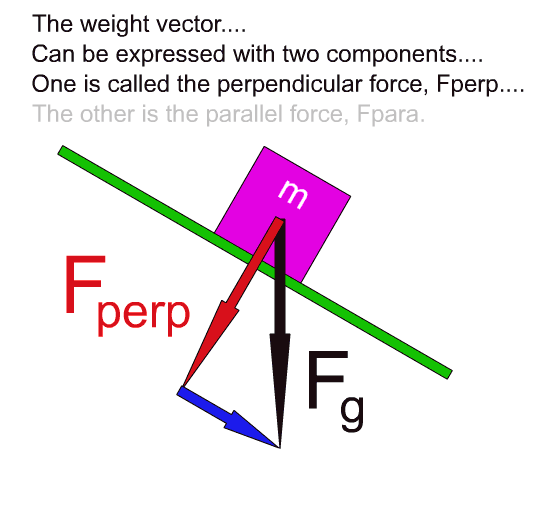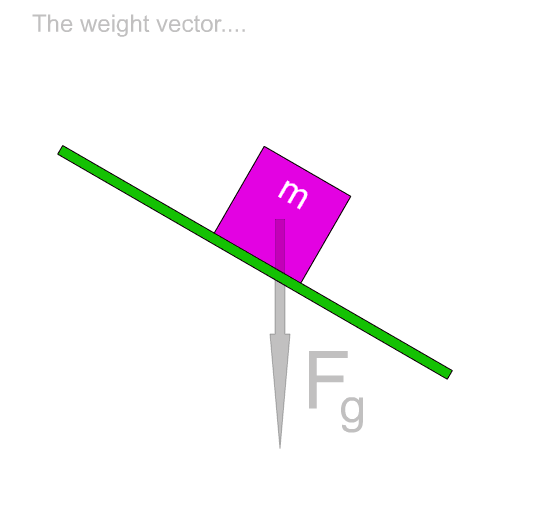
On the inclined plane the weight is considered as two components.
On the inclined plane the pull of gravity, or the weight of the object, does two things:
- The weight causes the object to push into and, if the object slides, to rub against the surface of the incline.
- The weight causes the object to be pulled down the slant of the incline.
The component that pushes the object into the surface is called the perpendicular force. The word perpendicular is used because this vector is aimed directly into the surface of the incline. The angle between it and the surface is 90 degrees. The symbol for the perpendicular force is:
Fperp
The component that pulls the object down the slanted surface is called the parallel force. It is called parallel because this vector lies along a line that is parallel to the surface of the inclined plane. The symbol for this force is:
Fpara
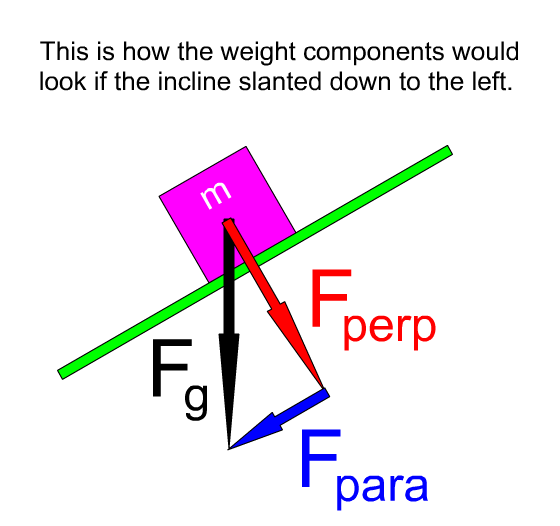
The ramp might be slanted 'the other way':
Another way to view the weight components:
An arrow symbol for a vector in a vector diagram can be moved about and remain valid as long as its size and direction do not change. Force vectors acting on an object are often presented with their tails at the center of that object. So in the following animation we show how the parallel force can be visualized this way. Perhaps seeing it this way helps to clearly get across the idea that it is this component force that is pulling the object down the slant of the incline.
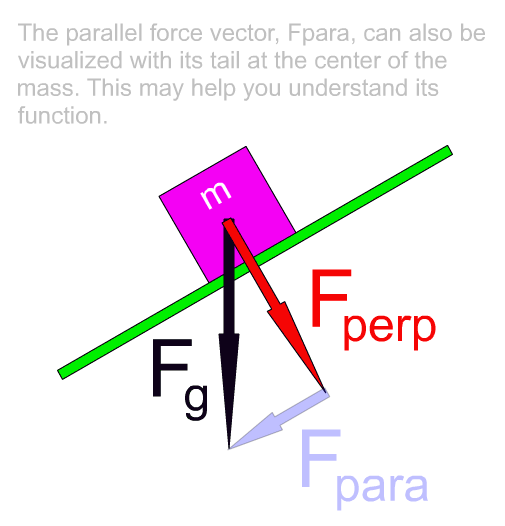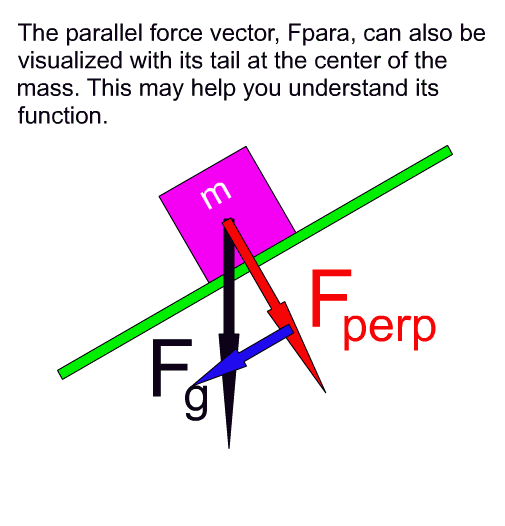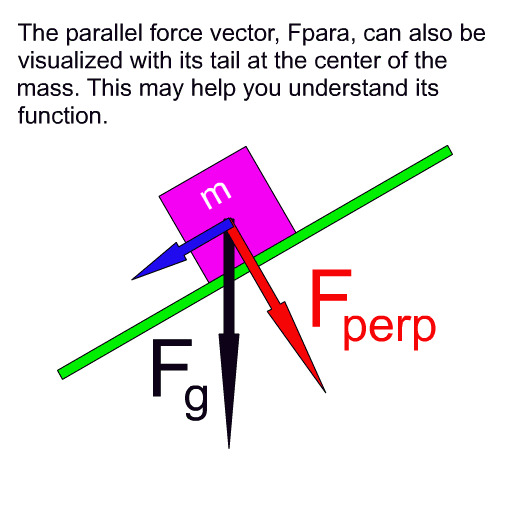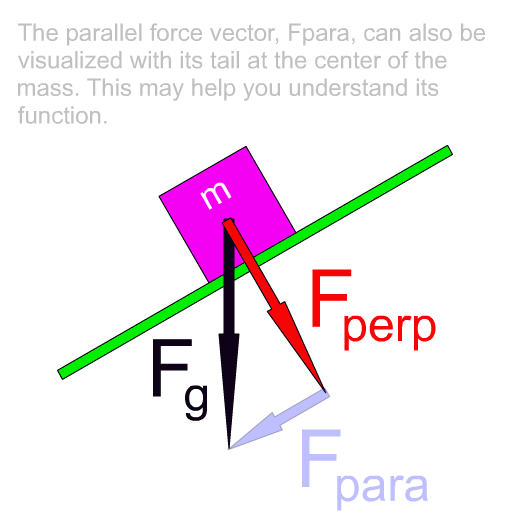
So, as it goes, if we draw the parallel force as a side to a right triangle, as we did at first, it helps us set up some trigonometry to solve for the sizes of the weight components. If we see it positioned with its tail centered on the object, as in the above animation, then it is easy to understand how this component is responsible for pulling the object down the slant of the inclined plane.
What these components do:
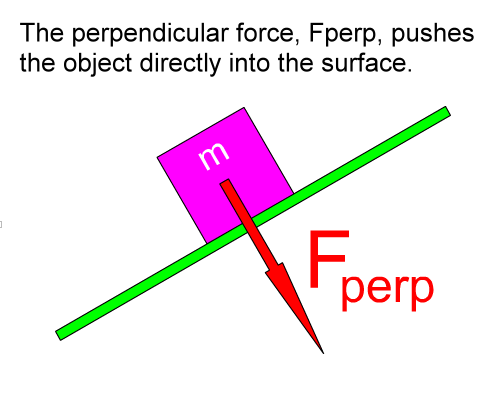
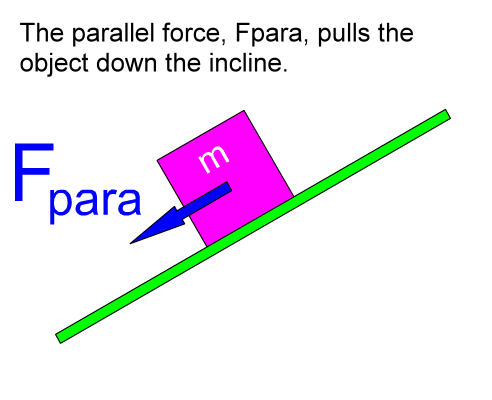
You might say that the two components of the weight each have a separate job to do. The perpendicular force component tries to push the object through the incline. The parallel force component tries to pull the object down the incline.
 |
 |
|
The component of the weight called the perpendicular force pushes the object into the surface of the incline. This force causes the bottom of the object to rub against the top of the incline's surface. If friction is considered, this force is important. The larger this force is, the larger friction will be. On a frictionless inclined plane, which we will be working with at first, this would not be a consideration. The object will not move in this direction unless the surface of the incline, or the ramp, is not strong enough to withstand this push. If the incline is strong enough, it will push back equally and oppositely to this perpendicular force and prevent the object from going this way. If the incline is not strong enough, like if you put an elephant on a ramp made of soda crackers, this force would crush the incline. |
The component of the weight called the parallel force pulls the object down the incline. Without friction, this force would cause the object to accelerate down the incline. If friction was present but less than this parallel force, then there would still be an acceleration down the incline, but it would be less of an acceleration than you would see on a frictionless inclined plane. In some cases static, or starting, friction could be greater than this parallel force, and the object would not start to move. |
Understanding the component triangle:
The weight vector, Fg, along with its two components, Fperp and Fpara, form a right triangle. An angle within this right triangle is the same as the angle of the incline, as we will show.
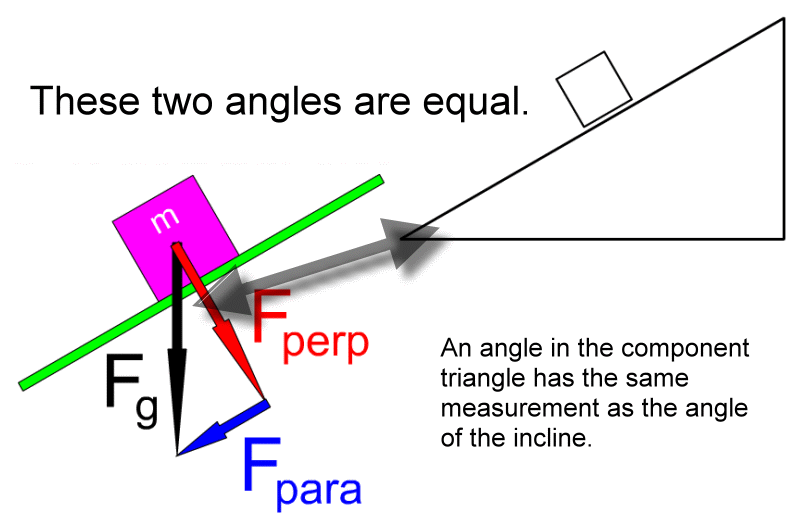
There must be several ways to show that the two angles shown above have equal measure. The following is a simple slide show that goes through one such proof. Click the small 'Next' link at the lower right in the slideshow.
Knowing the measurement for the angle within the component triangle opens the door to working with right triangle trigonometry and finding the values for these components.
Formulas for the inclined plane
The Greek letter theta is often used as a symbol for the angle of the incline.
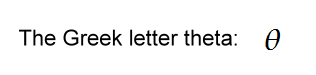
So a simple inclined plane diagram could look like this:
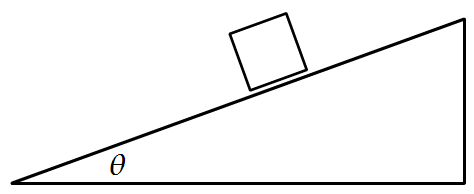
Now this angle theta is the same angle that appears in the weight component right triangle as shown in the diagram below. Note that the sides of this right triangle have been labeled so that we can use right triangle trigonometry (SOH-CAH-TOA) to solve this triangle.
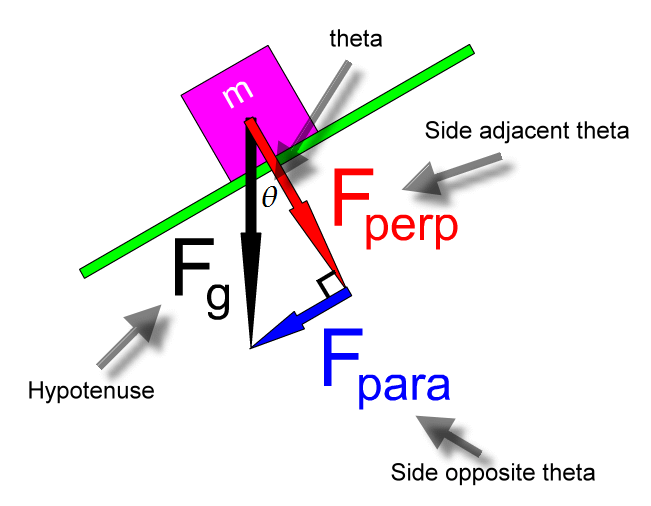
Derivation of the formula for the size of the parallel force:

Derivation of the formula for the size of the perpendicular force:

The parallel force:
So the size of the parallel force is calculated this way:
Fpara = Fg sin(theta)
Basically, the above formula states that the parallel force, that force that pulls the object down the slant of the incline, is equal to the weight of the object times the sine of the angle of the incline.
The perpendicular force:
And the size of the perpendicular force is:
Fperp = Fg cos(theta)
The above formula states that the perpendicular force, that force that pushes the object into the surface of the incline, is equal to the weight of the object times the cosine of the angle of the incline.
Substitution for weight:
We can write these two formulas in a slightly different form that is often useful. First remember the formula for the weight of a mass:
Fg = mg
By substituting (mg) for Fg in the two component formulas we have:
Fpara = (mg) sin(theta)
Fperp = (mg) cos(theta)
Example problem for the inclined plane:
An object with a mass of 2.5 kg is placed on an inclined plane. The angle of the incline is 20 degrees. What are the parallel force and the perpendicular force?
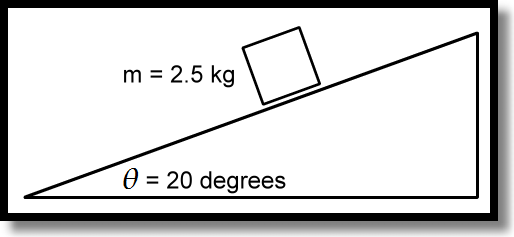
Solving for the parallel force:
Fpara = Fg sin(theta)
Fpara = (mg) sin(theta)
Fpara = (2.5 kg)(9.8 m/s2) sin(20 degrees)
Fpara = (24.5)(0.342)
Fpara = 8.4 N
The parallel force is equal to 8.4 N. So this object will be pulled down the slant of the incline with a force of 8.4 N.
Solving for the perpendicular force:
Fperp = Fg cos(theta)
Fperp = (mg) cos(theta)
Fperp = (2.5 kg)(9.8 m/s2) cos(20 degrees)
Fperp = (24.5)(.939)
Fperp = 23 N
The perpendicular force is equal to 23 N. This object will be pushed perpendicularly into the incline with a force of 23 N.
Going on:
When you are done with the material on this page you may want to continue with the following sections.