sin(a) = opp / hyp
sin(a) = o / h
sin(a) = sine
cos(a) = adj / hyp
cos(a) = a / h
cos(a) = cosine
tan(a) = opp / adj
tan(a) = o / a
tan(a) = tangent
Back Introduction Trigonometry Mathematics Contents Index Home
This demo shows you the right triangle trig function calculations for several angles, explanations below. Use the 'less' and 'greater' buttons to adjust the size of the angle. Notice how the values are calculated for each trig function depending upon the lengths of the sides of the triangle.
First of all, think of a trigonometry function as you would any general function. That is, a value goes in and a related singular value comes out. If that does not seem quite clear, go see The Definition of a Function and What is f(x)?
The names of the three primary trigonometry functions are:
| sine |
| cosine |
| tangent |
These are abbreviated this way:
| 'sin' for sine |
| 'cos' for cosine |
| 'tan' for tangent |
So, since we know the names of these functions, instead of writing f(x) , we will write:
| sin(x) |
| cos(x) |
| tan(x) |
Often, in general mathematics notation the parentheses are dropped from the above examples. Therefore, the notation will often look like this:
| sin x |
| cos x |
| tan x |
In Zona Land Education we will keep the parentheses.
Now, as usual, the input value is x. This input value usually represents an angle. For the sine function, when the input value is 30 degrees, the output value is 0.5. We would write that statement this way:
0.5 = sin(30 °)
Read: 'Zero point five is the sine of thirty degrees.'
Or:
sin(30 °) = 0.5
Read: 'The sine of thirty degrees is zero point five.'
Below is a listing of several popular input and output values for the three main trigonometry functions. You do not have to work at memorizing this table. After you use trigonometry for a while, these values will be remembered quite easily.
| 0.0000 = sin(0 °) | 1.0000 = cos(0 °) | 0.0000 = tan(0 °) |
| 0.5000 = sin(30 °) | 0.8660 = cos(30 °) | 0.5773 = tan(30 °) |
| 0.7071 = sin(45 °) | 0.7071 = cos(45 °) | 1.000 = tan(45 °) |
| 0.8660 = sin(60 °) | 0.5000 = cos(60 °) | 1.7320 = tan(60 °) |
| 1.0000 = sin(90 °) | 0.0000 = cos(90 °) | +infinity = tan(90 °) |
At this point our central issues will revolve around these questions:
| Where do these numbers come from? | |
| What do these numbers mean? | |
| Why, for example, is the cosine of 30 degrees equal to 0.8660? |
The input value for these trigonometric functions is an angle. That angle could be measured in degrees or radians. Here we will consider only input angles measured in degrees from 0 degrees to 90 degrees. The input values appear within the parentheses throughout the above table.
The output value for these trigonometric functions is a pure number. That is, it has no unit. This output value appears to the left of the equal sign throughout the above table.
There are several ways to understand why a certain input angle produces a certain output value. At first, the most important manner of understanding this is tied to right triangles. All of the trigonometric values for angles between 0 degrees and 90 degrees can be understood by considering this diagram:
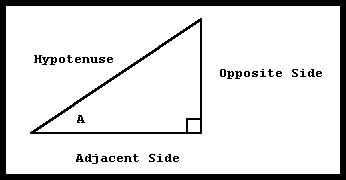
We will be concerned with angle A. Notice that the sides of the triangle are labeled appropriately 'opposite side' and 'adjacent side' relative to angle A. The hypotenuse is not considered opposite or adjacent to the angle A.
We will also be concerned with length of the three sides. For this discussion we will call the 'length of the opposite side' simply the 'opposite.' Similarly, the other two lengths will be called 'adjacent' and 'hypotenuse.'
The value for the sine of angle A is defined as the value that you get when you divide the opposite side by the hypotenuse. This can be written:
sin(A) = opposite / hypotenuse
Or simply:
sin(A) = opp / hyp
Or, even more simply:
sin(A) = o / h
Suppose we measure the lengths of the sides of this triangle. Here are some realistic values:
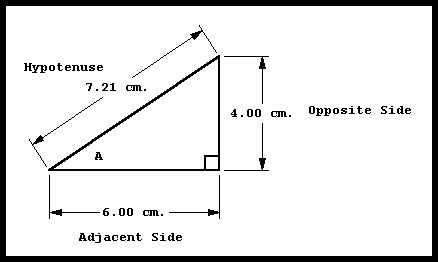
This would mean that:
sin(A) = opposite / hypotenuse = 4.00 cm / 7.21 cm = 0.5548
Or simply:
sin(A) = 0.5548
Now for the other two trig functions.
The value for the cosine of angle A is defined as the value that you get when you divide the adjacent side by the hypotenuse. This can be written:
cos(A) = adjacent / hypotenuse
Or:
cos(A) = adj / hyp
Or:
cos(A) = a / h
Using the above measured triangle, this would mean that:
cos(A) = adjacent / hypotenuse = 6.00 cm / 7.21 cm = 0.8322
Or simply:
cos(A) = 0.8322
The value for the tangent of angle A is defined as the value that you get when you divide the opposite side by the adjacent side. This can be written:
tan(A) = opposite / adjacent
Or:
tan(A) = opp / adj
Or:
tan(A) = o / a
Using the above measured triangle, this would mean that:
tan(A) = opposite / adjacent = 4.00 cm / 6.00 cm = 0.6667
Or simply:
tan(A) = 0.6667
The angle A in the above triangle is actually very close to 33.7 degrees. So, we would say:
| 0.5548 = sin(33.7°) |
| 0.8322 = cos(33.7°) |
| 0.6667 = tan(33.7°) |
So, suppose that you wanted to know the trigonometry values for 47.5 degrees? You could carefully draw a right triangle using a ruler and protractor that had an angle equal to 47.5 degrees in the position of angle A. Then, you could carefully measure the sides. Lastly you could divide the appropriate sides to find the values for the three trigonometric functions. You would find that:
| 0.7373 = sin(47.5°) |
| 0.6755 = cos(47.5°) |
| 1.0913 = tan(47.5°) |
Someone has already done this, in a way, for all the possible angles. All the input angles and output values are listed in tables called trig tables. They look like this:
| Angle | sin | cos | tan |
| 0.0 | 0.0000 | 1.0000 | 0.0000 |
| 0.5 | 0.0087 | 0.9999 | 0.0087 |
| 1.0 | 0.0174 | 0.9998 | 0.0174 |
And so on...
These let you look up the trigonometric values for any angle. Calculators and computers, of course, will let you do the same.
Below is again the triangle from the above diagrams, except now the other acute angle, B, is marked. Also marked are the sides that are adjacent and opposite to angle B.
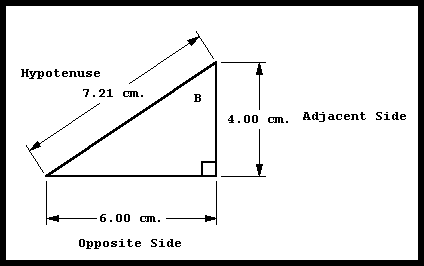
Here are the three trig functions for angle B:
| sin(B) = opposite / hypotenuse = 6.00 cm / 7.21 cm = 0.8322 |
| cos(B) = adjacent / hypotenuse = 4.00 cm / 7.21 cm = 0.5548 |
| tan(B) = opposite / adjacent = 6.00 cm / 4.00 cm = 1.5000 |
If you look carefully you will notice that the sine of angle B is the same value we calculated above for the cosine of angle A. You should also notice that the cosine of angle B is equal to previous calculation for the sine of angle A.
This is because the opposite side for angle B is the adjacent side for angle A, and because the adjacent side for angle B is the opposite side for angle A.
This is demonstrated in the following diagram:

We could summarize this relationship this way:
| sin(A) = A's opposite / hypotenuse = 4.00 cm / 7.21 cm = 0.5548 |
| cos(B) = B's adjacent / hypotenuse = 4.00 cm / 7.21 cm = 0.5548 |
| cos(A) = A's adjacent / hypotenuse = 6.00 cm / 7.21 cm = 0.8322 |
| sin(B) = B's opposite / hypotenuse = 6.00 cm / 7.21 cm = 0.8322 |
Now, angle A and B form a pair of complementary angles. That is, their measurements add up to 90 degrees. This is because the measurement of the interior angles for any triangle must sum to 180 degrees, and in this triangle 90 of those degrees are taken up by the right angle, so that leaves 90 degrees remaining from the total of 180 to be split up between angle A and B.
So, here we notice that the sine of an angle is equal to the cosine of its complement, and that the cosine of an angle is equal to the sine of its complement.
Also, we will take note of the relationship between the tangents of the complementary angles A and B. The tangent of angle A is equal to the reciprocal, or inverse, of the tangent of angle B, and, likewise, the tangent of angle B is equal to the reciprocal of the tangent of its complement, angle A. This is summarized in the following table:
| tan(A) = A's opposite / A's adjacent = 4.00 cm / 6.00 cm = 2/3 or about 0.6667 |
| tan(B) = B's opposite / B's adjacent = 6.00 cm / 4.00 cm = 3/2 or 1.5000 |
Note that 2/3 and 3/2 are reciprocals.
Here is an easy way to remember these relationships for trig functions and the right triangle. Just write down this mnemonic:
SOH - CAH - TOA
It is pronounced 'so - ka - toe - ah.'
The SOH stands for 'Sine of an angle is Opposite over Hypotenuse.'
The CAH stands for 'Cosine of an angle is Adjacent over Hypotenuse.'
The TOA stands for 'Tangent of an angle is Opposite over Adjacent.'
Back Introduction Trigonometry Mathematics Contents Index Home
