Additional Information About the Displacement and Acceleration Equation
Back Kinematics Equations Kinematics Mechanics Physics Math Contents Index Home
Here's our displacement equation:
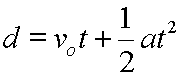
Other popular ways exist to write the symbols in this equation.
There are more than one symbol for the original velocity. All three of these symbols mean the same velocity:
| vo | Original velocity |
| vi | Initial velocity |
| v1 | First velocity |
So, this displacement equation could be written in any of these fashions:
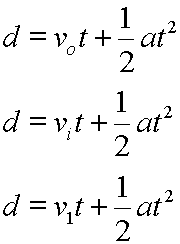
Now, displacement means change in position, and position is symbolized as delta x, so:
![]()
We can replace d with delta x:
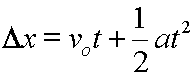
Often, when delta x is used in this fashion, you will also see the time period written as a delta quantity:
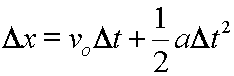
Since change in x works like any other delta quantity, change in position equals the final position minus the original position, as in:
![]()
So, replacing delta x with the right side of the above equation we get yet another form for our displacement equation:
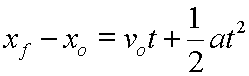
Doing a bit of algebra rearranging, (adding xo to each side), we can solve for the final position, which gives our last equation its more formal presentation:
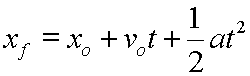
This form will tell you the final position of the object, (where it ends up), if you know its starting position, its starting velocity, its constant acceleration, and the time period for its acceleration.
A very good way to think about our original displacement equation is that it will give you the displacement at any given time. Of course, you need to know the original velocity and acceleration. They would be known fixed quantities, or constants in the problem.
Our original displacement equation can be thought of as a function. It would be the displacement as a function of time. In function notation, the equation would look like this:
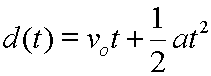
Also, if we want to consider position as a function of time, (that is, final position as a function of time), we can write:
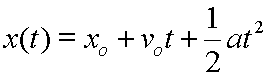
Here, the original position, xo, would be another known constant.
Lastly, the symbol s is often used instead of d for displacement. This symbol is usually seen a bit past the beginner's level. Using s for displacement, our equation would look like this:
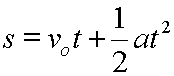
Back Kinematics Equations Kinematics Mechanics Physics Math Contents Index Home
