Displacement and Acceleration Algebra
Back Kinematics Equations Kinematics Mechanics Physics Math Contents Index Home
Here we will take a look at the equation that allows us to solve for displacement when the object is constantly accelerating. That equation looks like this:
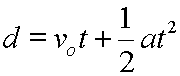
This equation would read:
Displacement equals original velocity times time plus one-half acceleration times time squared, (or times the square of time).
We will use algebra to solve the above equation for each of its variables.
The equation in its original form is already solved for displacement, d:
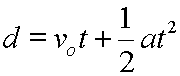
Here, we will solve for original velocity, vo:
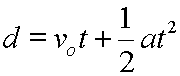 |
Start here. |
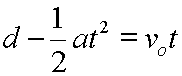 |
Subtract (1/2)at2 from each side. |
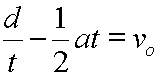 |
Divide each side by t. |
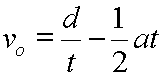 |
Rearrange by switching left and right sides. |
Now, let's see the equation solved for acceleration, a:
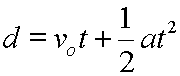 |
Start here. |
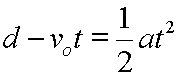 |
Subtract vot from each side. |
 |
Multiply each side by 2/t2. |
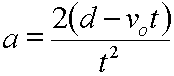 |
Rearrange by switching left and right sides. |
Solving for the time period, t, requires more algebra understanding than the above solutions. Let's take a look at this.
Notice that the equation:
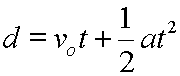
is actually a quadratic equation in t. This can be shown with a bit of rearranging.
First subtract d from each side. This produces the following:
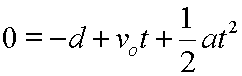
Next, rearrange the right side so that it looks like this:
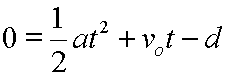
Clearly, we have a quadratic equation in t here, since the above equation has the form:
![]()
Where:
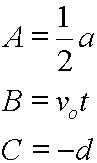
Now, the solution to:
![]()
is:
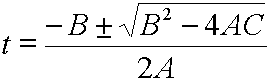
And, by substituting the above values for A, B, and C, we note that the solution to:
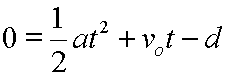
is:
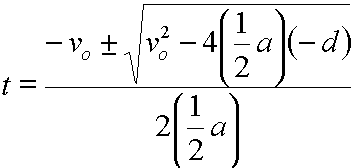
This last equation can be simplified to:
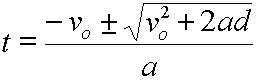
When using this last equation in kinematics problems, only positive values for t should be considered.
Note that solving for t is greatly simplified if vo equals zero:
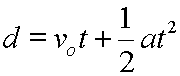 |
Start here. |
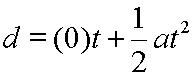 |
Let vo = 0. |
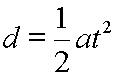 |
The first term drops out, since multiplication by zero yields zero. |
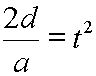 |
Multiply each side by 2/a. |
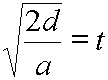 |
Take the square root of each side. |
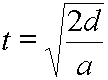 |
Rearrange by switching the left and right sides. |
So, here are our final algebraic rearrangements for the displacement and acceleration equation:
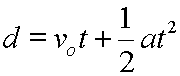 |
Solved for displacement, d. |
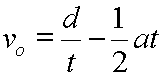 |
Solved for original velocity, vo. |
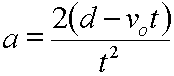 |
Solved for acceleration, a. |
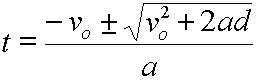 |
Solved for time, t. |
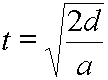 |
Easier solution for time when original velocity is zero. |
Back Kinematics Equations Kinematics Mechanics Physics Math Contents Index Home
