Time Independent Acceleration Algebra

Back Kinematics Equations Kinematics Mechanics Physics Math Contents Index Home

Here we will take a look at the equation that allows us to solve for several quantities when the object is accelerating. This particular equation is time independent; that is, time does not appear in the equation. The equation looks like this:

This equation would read:

Final velocity squared minus original velocity squared equals two times acceleration times displacement.

We will use algebra to solve the above equation for each of its variables.

The equation in its original form is not solved for any individual quantity:

Here, we will solve for final velocity, v_f:

	Start here.
	Add v_o² to each side.
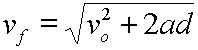	Take the square root of each side.

Here, we will solve for original velocity, v_o:

	Start here.
	Subtract v_f² from each side.
	Multiply each side by (-1).
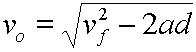	Take the square root of each side.

Now, let's solve for displacement, d:

	Start here.
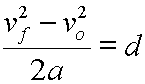	Divide each side by 2a.
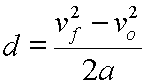	Rearrange by switching the left and right sides.

Lastly, let's solve for acceleration, a:

	Start here.
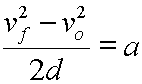	Divide each side by 2d.
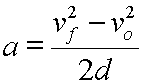	Rearrange by switching left and right sides.

Back Kinematics Equations Kinematics Mechanics Physics Math Contents Index Home

Custom Search