Origin of the Velocity and Acceleration Equation
Back Kinematics Equations Kinematics Mechanics Physics Math Contents Index Home
Here we will take a look at the derivation of the following kinematics equation:
![]()
The above equation solves for the final velocity of an object when it is undergoing a constant acceleration. You need to know the original velocity, vo, the constant acceleration, a, and the time period of the acceleration, t. These values are plugged into the equation, and the calculation results in the final velocity.
Actually, this equation can be thought of as a rearrangement of the definition of acceleration. So, we will start with the definition of acceleration which looks like this:
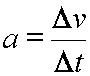
The above would be read:
Acceleration equals the change in velocity divided by the change in time.
Or:
Acceleration equals delta velocity divided by delta time.
Now, any delta quantity equals the final value for the quantity minus the original value for the quantity.
So, delta velocity, or change in velocity, equals the final velocity minus the original velocity. That is:
![]()
In like manner, delta time is the final time minus the original time.
This delta time, though, is simply the amount of time that passes while the velocity is changing.
We can symbolize this amount of time with a simple t. That is:
![]()
So, combining these meanings for delta velocity and delta time we get:
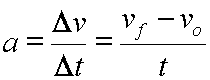
Or, simply stated:
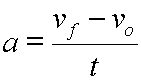
The rest of this derivation is simple algebra:
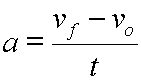 |
Start here. |
|
|
Multiply each side by t. |
|
|
Add vo to each side. |
|
|
Rearrange by switching left and right sides. |
We have derived our velocity equation for constant acceleration:
![]()
Back Kinematics Equations Kinematics Mechanics Physics Math Contents Index Home
