What Are Deltas?

Delta means 'change in.'

Delta looks like this:

In this discussion, as it relates to kinematics and the study of physics in general, the Greek letter delta means 'change in.'

The Greek letter delta, when used this way, looks like this:

It means 'change in'. So, if the variable x stands for position, then this notation:

is read 'change in position.' It could also be read 'change in x.'

If the variable v stands for velocity, then the following notation stands for 'change in velocity', or 'change in v':

And 'change in time' would look like this:

Now, any time there is a change in a quantity that change is calculated by taking the later value for that quantity and subtracting from it the earlier value for that quantity. So, for example, if an object were first at a position given by the coordinate 3 meters and later at a position given by the coordinate 8 meters, then its change in position would be calculated this way:

The first position at 3 meters would be called x₁, and the second position at 8 meters would be given by x₂. So, the complete notation demonstrating the calculation for the change in position would look like this:

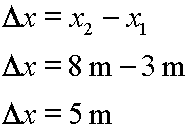
Therefore, we would say that the change in position was equal to 5 meters.

Note that changes in a quantity can be negative. If an object begins its movement at a coordinate of 9 meters and ends its movement at a coordinate of 3 meters, then the calculation for its change in position would look like this:

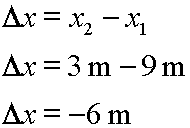
Our latest examples here have been with changes in position, but delta calculations proceed the same way with other quantities. Here's another example. If an object was moving with a velocity of 8.2 m/s originally and then changed its velocity to 3.6 m/s later, the calculation for the change in velocity would proceed this way:

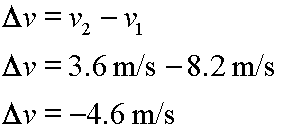
And, if an experiment started when time was 3.5 seconds and ended when time was 12.9 seconds, then this would be the calculation for the change in time, or the time period, for the experiment:

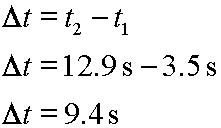
One note about the calculation for delta time: Unless you are working on some special time reversal problem, which would be unusual, but perhaps interesting; if you end up with a negative change in time, and you are working in classical Newtonian physics, then very most likely you have made a mistake.

So, in general, all delta quantity calculations proceed the same way. Take the later quantity and subtract from it the former quantity. Here, we show the calculation with an abstract quantity, 'it'.

Hopefully, even if you are unsure regarding the meaning of the following symbols, the delta calculations make sense:

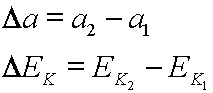
Ms. Explain comments on calculus.

In all of the above examples the subscript 1 and the subscript 2 were used to designate former and later respectively. The former value, (sub 1), is often called the original or initial value. And the later value, (sub 2), is often called the final value.

If we let the subscript 'o' represent the original value and let the subscript 'f' represent the final value, then the following notation can also be used for the change in position:

The above would be read: 'The change in position is equal to the final position minus the original position.' Or, it could be read as: 'Delta x equals x final minus x original.'

Here is similar notation for a change in time:

One can also use the subscript 'i', which means initial. Initial in this context is synonymous with original. The above notation for delta time could be also written as:

This would be read: 'The change in time is equal to the final time minus the initial time', or 'Delta t equals t final minus t initial.'

Basically, '1' and '2' form one group of subscripts. Another group is 'f', 'o', and 'i'. One should not mix notation from one group with another, as in:

Using position, or x, as an example, notice that by using algebra we can rearrange any of the above delta equations so that it solves for the first or the second value of the quantity. Specifically, if:

Then we can solve for x₂:

The above can be read: 'The second position equals the first position plus the change in position.' But, in general, regarding a delta equation for any quantity, think of it this way: 'The amount of a quantity that you end up with is the amount of that quantity that you started with plus the amount by which that quantity changed.' Certainly one can follow that the amount you have in your bank account after a deposit is equal to the amount you had before the deposit plus the amount of the deposit, and the above works the same with position coordinates.

And we can solve for x₁:

This could be read: 'The first position is equal to the second position minus the change in position.' But, again, see this equation as it might apply to any quantity and also notice: 'The amount of a quantity that you started out with is equal to the amount of the quantity that you ended up with minus the amount of change which that quantity experienced.'

So, in summary:

• The Greek letter delta, , means 'change in'.
• This 'change in' refers to a change in the value of some quantity.
• The change is calculated by subtracting the earlier value of the quantity from the later value of the quantity.
• This subtraction may yield a positive or a negative or zero change result.
• You can use the subscripts '1' and '2' to refer to the first and second values respectively.
• You can use the subscripts 'o', 'i', and 'f' also. The subscripts 'o' and 'i' mean original and initial respectively, and the subscript 'f' means final.

Also, closing note:

• The Greek letter delta can appear in other contexts and have other meanings. It can appear upper case or lower case, written as print or script. For example, lower case script delta is often used as a symbol for an angle, and in advanced calculus lower case script delta is used in the symbol for a partial derivative. But when delta is used as explained above, in upper case print, it always means 'change in'.