Definition of Momentum

Importance of Momentum.

Momentum is a corner stone concept in Physics. It is a conserved quantity. That is, within a closed system of interacting objects, the total momentum of that system does not change value.

This allows you to calculate and predict outcomes when objects bounce into one another. Or by knowing the outcome of a collision, you can figure out what was the initial state of the system.

The type of momentum which we will be covering here is called linear momentum. In classical physics this is the momentum of a mass (an object) as it moves along a straight line.

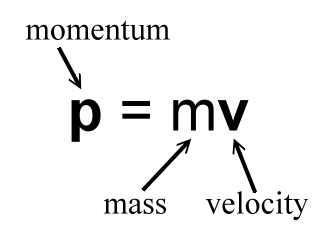
Momentum is mass times velocity.

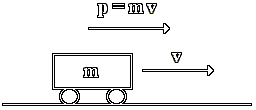When an object is moving, it has a non-zero momentum. If an object is standing still, then its momentum is zero.

To calculate the momentum of a moving object multiply the mass of the object times its velocity. The symbol for momentum is a small p.

A sample momentum calculation.

In the above picture, let's say that the mass is 2.0 kg and that the velocity is 4.0 m/s. That is:

To calculate the momentum for this object we will multiply the mass times the velocity:

So, the momentum of the object is calculated to be 8.0 kg-m/s.

Note the unit for momentum. It is 'kg-m/s'. This is pronounced 'kilogram meter per second'. The dash is not pronounced.

Momentum is a vector.

Momentum is a vector. That means that momentum is a quantity that has a magnitude (or size) and a direction.

The above problem is a one dimensional problem, so the object is moving along a straight line. In situations like this the momentum is usually stated to be positive to the right, and negative to the left.

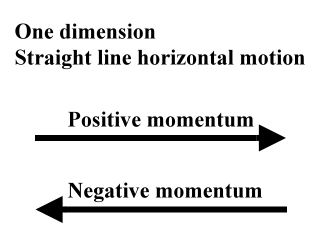
 So, in the above problem you would say that the momentum is 'positive 8.0 kg-m/s', or '8.0 kg-m/s to the right'. Usually, though, in simple cases like this we just say that the momentum is '8.0 kg-m/s' with the positive sign understood.

If the object was moving toward the left with a velocity of -4.0 m/s, then the momentum would be -8.0 kg-m/s, and you would say 'negative 8.0 kg-m/s'.

Momentum problems can become more complicated, however. You can calculate momentum in two and three dimensions. Under these conditions, say in a two dimensional problem, you would state a momentum using language such as '3.0 kg-m/s in a direction of 50 degrees North of East'.

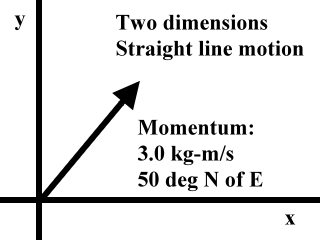
At first, though, our momentum problems will be in only one dimension. We will imagine objects traveling in a straight line moving toward the right (positive) or left (negative).

Momentum is not velocity.

Sometimes the concept of momentum is confused with the concept of velocity. Do not do this. Momentum is related to velocity. In fact, they both have the same direction. That is, if an object has a velocity that is aimed toward the right, then its momentum will also be directed to the right. However, momentum is made up of both mass and velocity. You must take the mass and multiply it by the velocity to get the momentum.

Momentum is directly proportional to velocity.

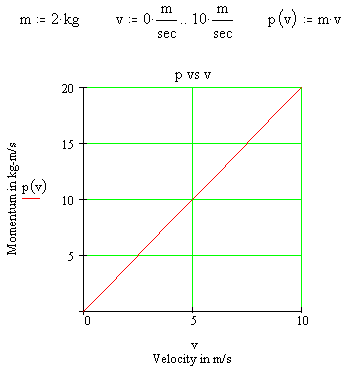If the mass is kept constant, then the momentum of an object is directly proportional to its velocity. In the example at the left, the mass is kept constant at a value of 2.0 kg.

The velocity changes from 0 m/s to 10 m/s while the momentum changes from 0 kg-m/s to 20 kg-m/s. This creates a straight line graph when momentum is plotted as a function of velocity. (The symbol for momentum as a function of velocity would be p(v).) The straight line graph demonstrates a direct proportion between momentum and velocity.

So if you were to double the velocity of an object, then the momentum of that object would also double. And, if you were to change the velocity of an object by a factor of 1/4, then the momentum of that object would also change by a factor of 1/4.

Momentum is directly proportional to mass.

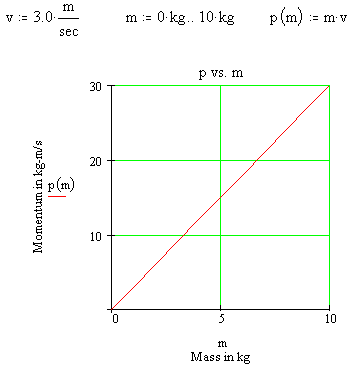If the velocity is kept constant, then the momentum of an object is directly proportional to its mass. In the example at the left, the velocity is kept constant at a value of 3.0 m/s.

The mass changes from 0 kg to 10 kg while the momentum changes from 0 kg-m/s to 30 kg-m/s. This creates a straight line graph when momentum is plotted as a function of mass. (The symbol for momentum as a function of mass would be p(m).) The straight line graph demonstrates the direct proportion between momentum and mass.

For example, if you were to triple the mass of an object, then the momentum of that object would also triple. And, if you were to change the mass of an object by a factor of 1/2, then the momentum of that object would also change by a factor of 1/2.