Spring Potential Energy (Elastic Potential Energy)

Definition of Spring Potential Energy (Elastic Potential Energy)

If you pull on a spring and stretch it, then you do work. That is because you are applying a force over a displacement. Your pull is the force and the amount that you stretch the spring is the displacement.

Since work is the transfer of energy, we must understand where the energy was transferred. We say that the energy was transferred into the spring. The work becomes stored energy in the spring. The work becomes potential energy in the spring.

A spring can be stretched or compressed. The same mathematics holds for stretching as for compressing springs. We will be primarily discussing energy as it is stored in a spring when it is stretched here; however, the same physics would apply for a spring when it is compressed.

As you have probably noticed from the above header, spring potential energy is also called elastic potential energy.

Linear Springs

This discussion will be about linear springs, the simplest type of spring.

A linear spring is a spring where the force that stretches the spring is in direct proportion to the amount of stretch. That is, the force vs. extension graph forms a straight, positively sloped line that passes through the origin, like this:

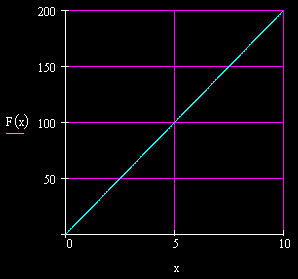
The slope of this graph is called the spring constant and is symbolized by the letter k. The spring constant in the above graph is 20 Newtons per meter, or 20 N/m. This means that you would need 20 Newtons of force to stretch the spring one meter, or 2 Newtons of force to stretch the spring 0.1 meter, and so on.

Work Done Stretching The Spring

Let us say that in this discussion a force of F is necessary to stretch the spring to an extension of x.

We see below that this force F and the related extension x have been marked on the graph. Also detailed is the area under the graph for this situation.

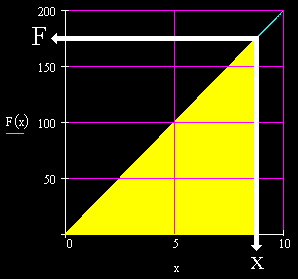
The area under this graph of force vs. extension is in Joules, units of energy. This is because the area is in units of Newtons (vertically) times meters (horizontally).

Do not forget that units of work are units of force times units of displacement, or units of Newtons times units of meters. And units of work are units of the transfer of energy, that is, they are units of energy, or Joules.

So, the area under this graph symbolizes energy. This area is the work done to stretch the spring.

Now, work is the transfer of energy. After the spring has been stretched, and work has been done, to where has the energy been transferred? We say that it has become potential energy in the spring. That is, the energy has been stored in the spring. Therefore, the amount of energy symbolized by the area under the above graph is the energy that has been stored in the spring. It is the potential energy of the spring.

This area can be calculated. It is shaped like a triangle; so, its area is one half times its height times its base. We have:

Area under graph = (0.5)(F)(x)

This area is the energy stored in the spring. The symbol for the energy stored in the spring could be U_s. The 'U' stands for potential energy and the subscript 's' stands for spring. So, now we have:

U_s= (0.5)(F)(x)

The spring is a linear spring where the stretching force is directly proportional to the extension, as mentioned above. This, again, can be stated as:

F = kx

Placing this substitution for F in the above formula for U_s we get:

U_s= (0.5)(kx)(x)

Removing the parentheses and noticing that x times x is x², we have:

U_s= 0.5kx²

This last formula reads: The potential energy of a spring, or the energy stored in a spring, equals one half times the spring constant times the square of the extension. This is how to calculate how much energy is stored in a spring.

Work Done Compressing The Spring

Some linear springs store energy through compression, rather than extension. For example, when you compress the spring in a common jack-in-the-box toy, you do work on the spring, and that work is stored as energy in the spring. Later, when the jack-in-the-box pops, that energy comes out of storage.

The formula for the amount of energy stored in a linear spring due to compression is the same as the one for extension:

U_s= 0.5kx²

Questions about Spring Potential Energy

Here are a few problems over the above equations.