Origin of the Time Independent Acceleration Equation

Back Kinematics Equations Kinematics Mechanics Physics Math Contents Index Home

Here we will take a look at the derivation of the following kinematics equation:

 

This equation in its above form is not solved for any particular variable.

 

Notice that it relates four quantities: final velocity, v_f, original velocity, v_o, constant acceleration, a, and displacement, d. Using algebra you can rearrange this equation to solve for any one of those quantities. That algebraic rearrangement is covered here.

 

What is important to notice is that the quantity of time is not present in this equation. We say, therefore, that the equation is time independent.

This equation is often useful in kinematics problems where you do not know the time period of the acceleration but still have to work with the velocities, acceleration, and displacement.

 

We derive this equation by combining the other two kinematics equations in this section, and, through substitutions, eliminating the time variable.

Here are the other two equations; first, the displacement equation:

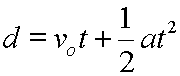
And second, the velocity equation:

 

For the substitution this velocity equation is rearranged so that it is solved for t:

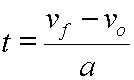
The above expression for t can be substituted into the displacement equation, and the resultant equation can be simplified and arranged till our time independent equation takes form.

 

The algebra for this is a bit more complicated than the algebra in our other examples. We will step through it as follows.

Let's start here:

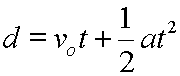
In the above equation we will substitute the following expression for t:

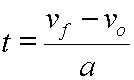
This gives us:

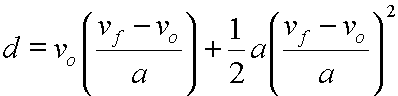
And on the right side of the equation in the second term, since the square of a fraction equals the square of the numerator over the square of the denominator, we get:

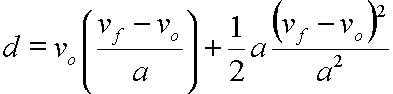
Multiplying each side by a,

Carefully canceling where a/a=1 and a²/a²=1,

We get:

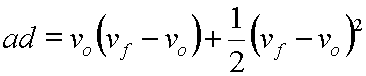
Now, on the right side, first term we distribute v_o into the parentheses and get:

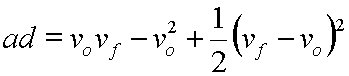
On the right side, third term, by expanding (v_f - v_o)² we get:

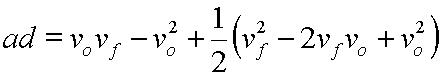
For reasons that are really only cosmetic, inside of that expansion we will note that v_fv_o=v_ov_f:

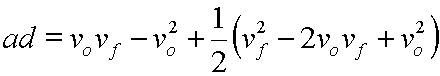
On the right side, third term we will distribute the 1/2 into the parentheses:

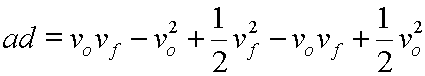
On the right side noting that v_ov_f cancels with -v_ov_f we get:

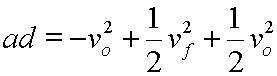
Now, multiplying each side by 2:

On the right side, since -2v_o²+v_o²=-v_o²:

Commuting terms on the right side we get:

And, lastly, we rearrange by switching the left and the right sides of the equation:

Back Kinematics Equations Kinematics Mechanics Physics Math Contents Index Home