Area of the v vs. t Graph, Change in position
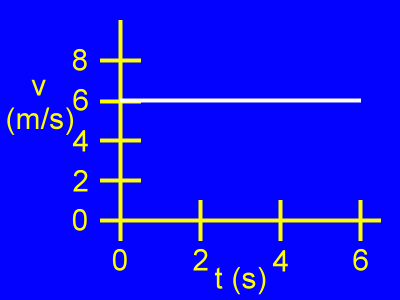
Here we see a velocity vs. time graph, or a v vs. t graph.
Velocity (v) is vertical.
Time (t) is horizontal.
The object is moving at a constant velocity of 6 m/s as the time passes from 0 s to 6 s.
Let's understand the meaning of the area of this graph.
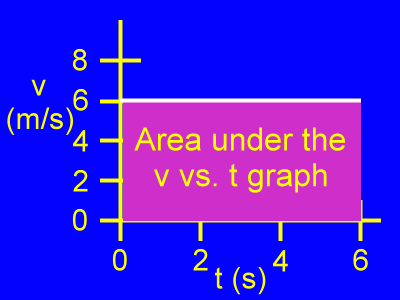
This is the area under this v vs. t graph.
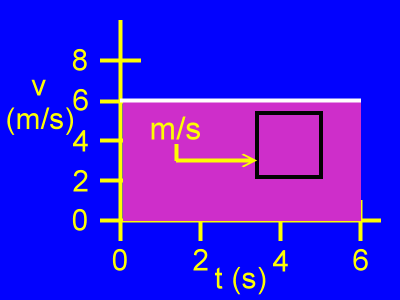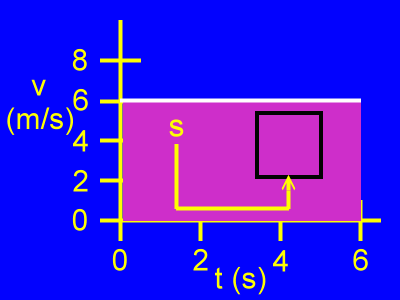
If we examine a section of this area, we notice that vertically it is measured in units of meters per second.
We also notice that horizontally it is measured in units of seconds.
The actual unit for the area will be units of meters per second times seconds. This comes out to be units of meters.

Here we see that along one edge of the area the units are meters per second. Along the other edge the units are seconds.
When values measured in these two units are multiplied to find the area, the result has units of meters per second times seconds. This results in a unit for meters. The seconds cancel.
Therefore, this area is in units of meters. It stands for displacement, or change in position, which is measured in meters.
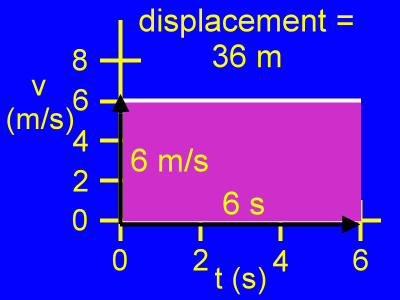
Here is the way an actual calculation for the displacement of an object would proceed given this v vs. t graph for the object's motion:
For the time period from 0 s to 6 s the area under the v vs. t graph is a rectangle. This rectangle is 6 m/s tall, and it is 6 s long.
Therefore, the area is equal to 6 m/s times 6 s, or 36 m.
36 m = (6 m/s)(6 s)
The displacement, or change in position, for this object is 36 meters.
displacement = change in position = delta x = Δx = 36 m