XVA - Constant Position

Back XVA Library Home XVA Kinematics Physics Contents Index Home


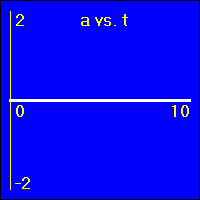
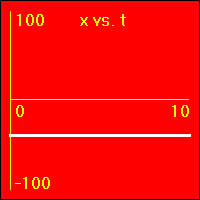
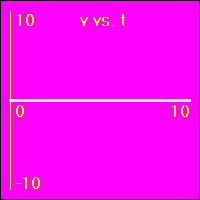
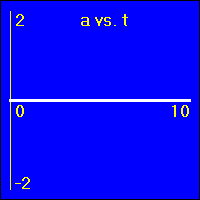
Here we are looking at the simplest type of motion, that of an object which is standing still. Perhaps many people would not even consider this a type of motion, but it is a starting point from which to understand more complicated motions.

 

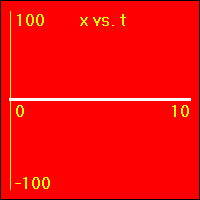
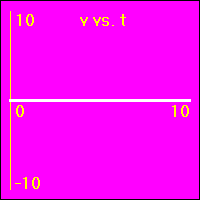
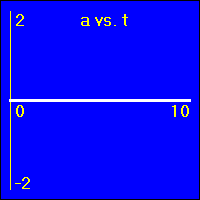
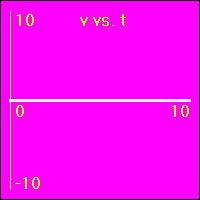
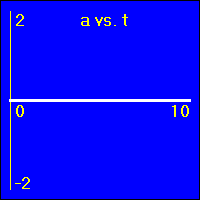
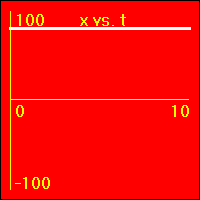
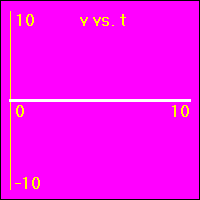
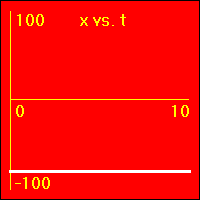
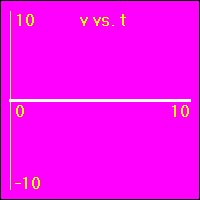
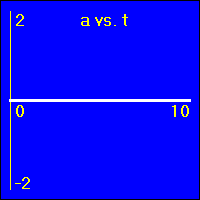
[1] Here is the first of our constant position examples. The object is resting at the origin of its position number line, and time is passing. It is standing still at x = 0.0 m.

Back
xo = 0.0 m vo = 0.0 m/s a = 0.0 m/s2
x vs. t graph v vs. t graph a vs. t graph
The object's position starts at 0.0 m, and it stays at that location as time passes. The object's velocity starts at 0.0 m/s. It's velocity remains at that value as time passes. The constant acceleration is 0.0 m/s2; so, the velocity does not change as time passes.
[1] XVA demonstration

Comments:

  • The object is standing still.
  • In all three of the above graphs the graph line of the function is drawn directly over the time axis. So, it may at first be difficult to see that there is actually data shown on these graphs.

 

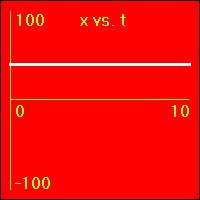
[2] The object here is also standing still. Unlike the object in [1] above, this object is not located at the origin. It starts out 40.0 meters away from the origin in the positive direction. It stays there.

Back
xo = 40.0 m vo = 0.0 m/s a = 0.0 m/s2
x vs. t graph v vs. t graph a vs. t graph
The object's position starts at 40.0 m, and it stays at that location as time passes. The object's velocity starts at 0.0 m/s. It's velocity remains at that value as time passes. The constant acceleration is 0.0 m/s2; so, the velocity does not change as time passes.
[2] XVA demonstration

Comments:

  • The object is standing still at a place 40.0 m from the origin.

 

[3] Here, again, the object is motionless. It is located at positive 80.0 meters from the origin.

Back
xo = 80.0 m vo = 0.0 m/s a = 0.0 m/s2
x vs. t graph v vs. t graph a vs. t graph
The object's position starts at 80.0 m, and it stays at that location as time passes. The object's velocity starts at 0.0 m/s. It's velocity remains at that value as time passes. The constant acceleration is 0.0 m/s2; so, the velocity does not change as time passes.
[3] XVA demonstration

Comments:

  • Again, the object standing still at another place. Now it's standing at x = 80. This is much like the object that is standing still in example [2].

 

[4] Be sure you understand what we mean by negative positions. Here, the object is remaining motionless and located at x = -40.0 meters. It is on the other side of the origin than the side it was on in the above three examples.

Back
xo = -40.0 m vo = 0.0 m/s a = 0.0 m/s2
x vs. t graph v vs. t graph a vs. t graph
The object's position starts at -40.0 m, and it stays at that location as time passes. The object's velocity starts at 0.0 m/s. It's velocity remains at that value as time passes. The constant acceleration is 0.0 m/s2; so, the velocity does not change as time passes.
[4] XVA demonstration

Comments:

  • The object is motionless located at a position coordinate of -40 m.
  • Note that the object's original position can be at a negative or a positive coordinate.
  • Usually, problems are set up considering the object to be starting at the origin. But that is not always the case, nor is it always desirable to set up a problem that way. So, be sure to understand what is meant by having the object start at a positive or negative position.

 

[5] This is another example of an object standing still at a negative position. Here, the object is remaining motionless and located at -80.0 meters.

Back
xo = -80.0 m vo = 0.0 m/s a = 0.0 m/s2
x vs. t graph v vs. t graph a vs. t graph
The object's position starts at -80.0 m, and it stays at that location as time ticks on. The object's velocity starts at 0.0 m/s. It's velocity remains at that value as time ticks on. The constant acceleration is 0.0 m/s2; so, the velocity does not change as time ticks on.
[5] XVA demonstration

Comments:

  • Another object standing still at another negative coordinate position. This is much like the object that is standing still in example [4].

Back XVA Library Home XVA Kinematics Physics Contents Index Home



Custom Search