Origin of the Displacement and Acceleration Equation

Back Kinematics Equations Kinematics Mechanics Physics Math Contents Index Home


Here we will take a look at the derivation of the following kinematics equation:

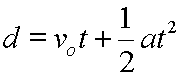
displacement equals velocity original times time plus one half times acceleration times time squared

The above equation solves for the displacement of an object when it is undergoing a constant acceleration. You need to know the original velocity, vo, the constant acceleration, a, and the time period of the acceleration, t. These values are plugged into the equation, and the calculation yields the displacement.

We will use a bit of reasoning and algebra to understand where this equation comes from.

 

First, let's consider the following velocity vs. time graph which shows a constant acceleration:

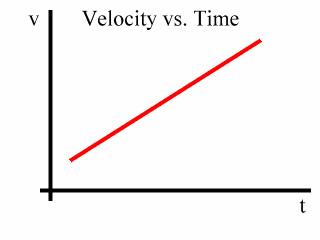
Since the slope of this graph is the acceleration, and since the slope of this graph is constant, the acceleration represented here is constant.

Also, remember that the area under this graph is the displacement, or change in position, of the object.

 

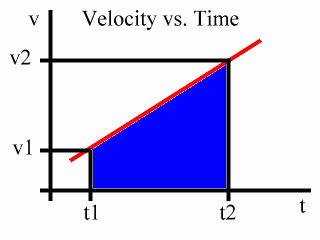
Now, let's consider a time period over which this acceleration occurs. We will concern ourselves with a time period from t1 to t2:

 

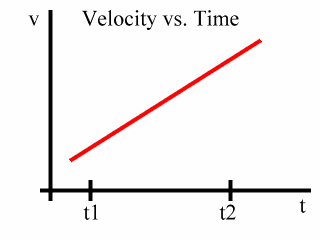
At t1 we will say that the velocity is v1.

And at t2 we will say that the velocity is v2:

 

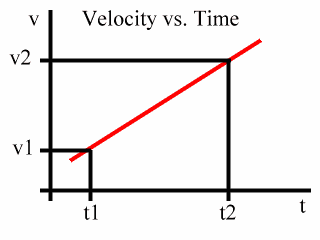
Now, recall that the area under this graph is the displacement of the object. So the area under the graph from t1 to t2 represents the displacement of the object over the time period from t1 to t2.

Notice that this area is a trapezoid, here shaded blue:

 

In general, the area of a trapezoid equals one-half times the sum of the bases times the height. This trapezoid, one might say, is "on its side" since the bases are vertical and the height is horizontal.

Here is an animated diagram of a generic trapezoid of this type. This diagram demonstrates how to find the area:

 

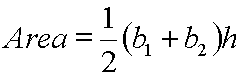Now, back to our v vs. t graph.

Notice that Base 1 is v1, Base 2 is v2, and that the Height is the time period from t1 to t2. This is shown in the following animated diagram:

 

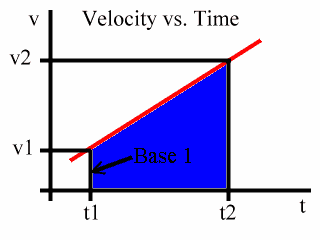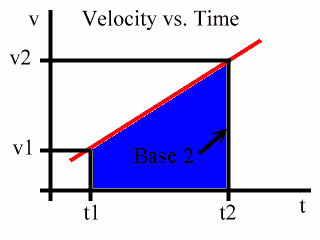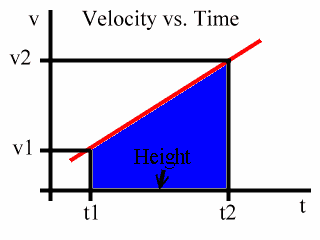
We will call the time period from t1 to t2 to be simply t. That is:

t = t2 - t1

So, the height of the trapezoid is t, and the two bases are v1 and v2. Therefore, the area of the trapezoid is:

Area = (1/2)(v1 + v2) t

 

Now, we remember that the area of a v vs. t graph is the change in position, or the displacement, and that displacement is symbolized with d.

Therefore, this:

Area = (1/2)(v1 + v2) t

Becomes:

d = (1/2)(v1 + v2) t

 

Now, as far as the acceleration over the time period t is concerned, v1 is the velocity at the start of the acceleration. That is, v1 is the first or original velocity; so, the symbol v1 and the symbol vo mean the same thing; that is:

vo = v1

And v2 is the velocity at the end of the acceleration. That is, v2 is the final velocity, and the symbols v2 and vf mean the same thing:

vf = v2

So, this:

d = (1/2)(v1 + v2) t

Is the same as:

d = (1/2)(vo + vf) t

 

We will now use another kinematics equation, and substitute it into our displacement equation. This other equation is:

vf = vo + at

See where the above equation comes from.

For the substitution we will place the expression (vo + at) into the displacement equation where vf appears. So, this:

d = (1/2)(vo + vf) t

Becomes this:

d = (1/2)(vo + vo + at) t

 

The rest is algebra:

d = (1/2)(vo + vo + at) t Start here.
d = (1/2)(2vo + at) t Since 2vo = vo + vo.
d = ((1/2)2vo + (1/2)at) t Distribute the (1/2).
d = (vo + (1/2)at) t Since (1/2)2 = 1.
d = (vot+ (1/2)at2) Distribute the t.
d = vot+ (1/2)at2 Remove some parentheses, and we are done.

 

We have derived our displacement equation for constant acceleration:

 

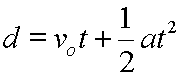
Back Kinematics Equations Kinematics Mechanics Physics Math Contents Index Home



Custom Search