Finding the Components of a Vector

The parts of a vector are the components of a vector.

The word components, in the following context, means parts. So, to talk about the components of a vector, we mean the parts of a vector.

For a great amount of situations the important parts of a vector are it's x-part and its y-part, or its x-component and its y-component. Here we will see how to find the x-component and the y-component of a vector.

The vector we will use in the following discussion is a force vector. The methods shown here, though, are true for any vector, such as a displacement, velocity, or acceleration vector.

To see an interactive demonstration showing several ways to visualize x- and y-components of a vector see the Components of a Vector page.

Also, you could visit the Force Component Machine and see how this all applies to a two dimensional force vector.

 

Force vector example

Here on the (x, y) set of axes is the force vector that we will be dealing with:

 

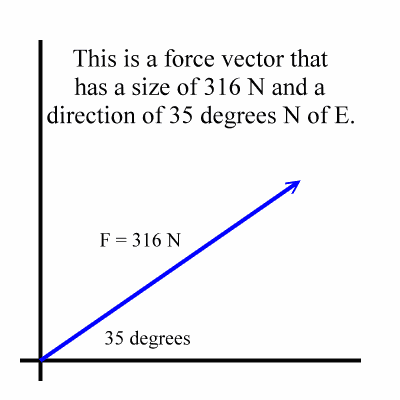
Seeing the x-component

If you drop a line from the tip of the original vector straight down to the x-axis and draw a vector along the x-axis from the origin to where this line hits the x-axis, then this newly drawn vector is the x-component of the original vector. In the diagram the line that was dropped down is shown as a thin black line and the x-component is shown as a red vector:

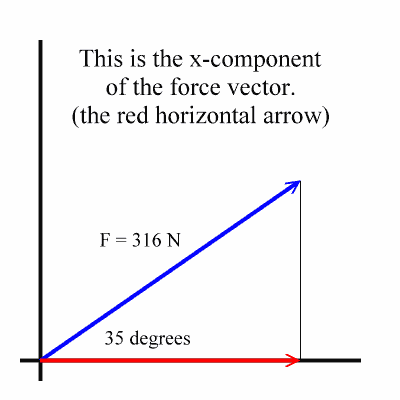
The tip of the x-component vector is directly below the tip of the original vector.

 

Seeing the y-component

In the following diagram the thin black horizontal line marks how high up the original vector rises. A vertical vector, (parallel to the y-axis), which rises to this height is called the y-component of the original vector. The y-component is shown below in green:

 

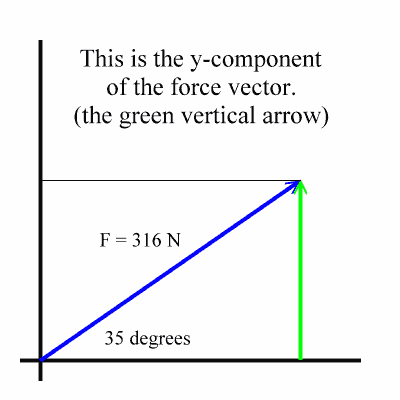
The x- and y-components form a right triangle.

When both the x-component and the y-component are drawn, a right triangle is formed with the original vector being the hypotenuse:

 

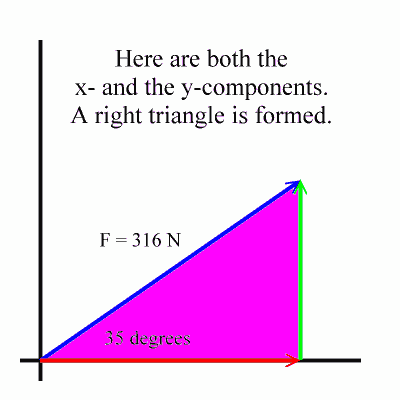
You can calculate the sides of the triangle using trigonometry.

This right triangle will allow us to to do right triangle trigonometry using SOH-CAH-TOA definitions. Those definitions are briefly explained here, and they are explained in much more depth in the Right Triangle Trigonometry section in the Trigonometry Realms of Zona Land.

Here we will use the Greek letter theta to represent an acute angle in a right triangle. The letter theta looks like this:

Here are the right triangle definitions for the sine, cosine, and tangent of an acute angle in a right triangle:

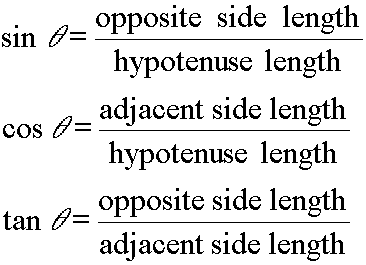
Usually we just summarize these three definitions with these three short sentences:

Again, if these definitions are new material, see the Right Triangle Trigonometry section for more information.

 

Here, the x-component is adjacent and the y-component opposite to the angle.

Now, let's get back to our right triangle formed by the original vector and its x-component and y-component. Here's the diagram, fully labeled:

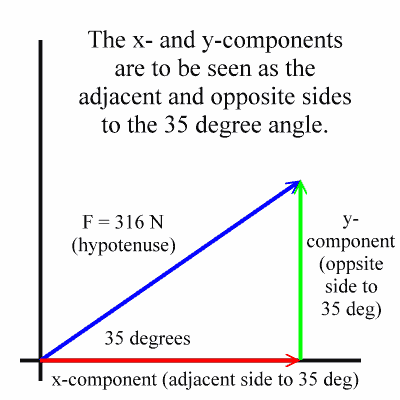
Notice that the x-component forms the side adjacent to the 35 degree angle, and that the y-component forms the opposite side to the 35 degree angle.

 

This is how to calculate the value for the x-component.

Let's find the size of the x-component; that is, let's find the size of the adjacent side.

We know the hypotenuse, (316 Newtons), and we know the angle, (35 degrees). We want to find the length of the adjacent side, (x-component). What trigonometry function relates the hypotenuse, an acute angle and its adjacent side in a right triangle? The cosine function does. The math looks this way:

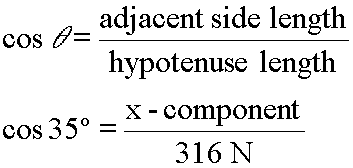
Now, since the original vector is named F, its x-component is named F_x. This would be read 'F sub x'. So, in the above math we should remove 'x-component' and replace that term with F_x, as in:

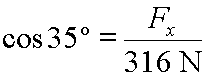
We can solve for F_x by doing a little algebra and looking up the cosine of thirty-five degrees:

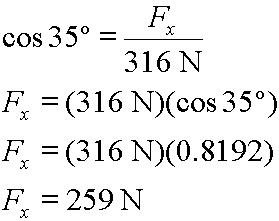
So, the x-component of the original vector is equal in size to 259 Newtons.

Now, realize this: The method for finding the x-component described here will not tell you the sign, (+ or -) for its value. This method will only tell you the size of the component. Notice that the x-component is pointing to the right. This makes it a positive x-component. (It would be negative if it pointed to the left.) So, we would would finally conclude that the x-component has a size of positive 259 Newtons.

 

This is the calculation for the y-component.

Okay, now let's find the size of the y-component; that is, let's find the size of the opposite side.

Again, we know the hypotenuse, (316 Newtons), and we know the angle, (35 degrees). We want to find the length of the opposite side, (y-component). It is the sine function that relates the hypotenuse, an acute angle and its opposite side in a right triangle. The math looks this way:

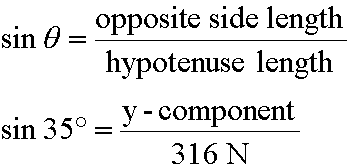
Now, since the original vector is named F, its y-component is named F_y which would be read 'F sub y'. So, in the above math we should remove 'y-component' and replace that term with F_y, as in:

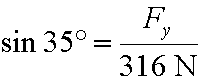
We can solve for F_y much like we solved for F_x:

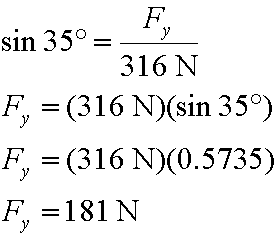
So, the y-component of the original vector is equal in size to 181 Newtons.

Again, like in the case of the x-component, we must look at the diagram to correctly interpret the sign, (+ or -), of this y-component. This y-component is pointing up, so it is positive. (It would be negative if it pointed down.) Finally, we conclude that the y-component has a size of positive 181 Newtons.

 

Related material

Again, to see the many ways that vectors can be drawn or visualized, look at the Components of a Vector page, and be sure to see the Force Component Machine to see how this all works out for force vectors.