Expression Evaluation, Introduction to Expressions
In a very simple manner, this certainly seems true:
|
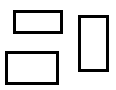
As many of these circles |
equals |
as many of these rectangles. |
 |
 |
So, how do we talk about and write about 'as many of' or 'how many'?
One way to do it is with words. Using words, here's how many circles there are above:
Three
Mathematicians usually do not use words for these types of situations, however. They prefer other ways.
Another way to describe how many circles we have here is to use digits. Here's how many circles using digits:
3

When digits are used to describe 'how many' we often say we are dealing with numbers. Of course, numbers can have more than one digit, and they may include a decimal point. They can also include a positive or a negative sign, but in some discussions those are not considered part of the number, but are considered an operator on the number. More about that later.
Now, 'three' or '3' is said to be the value a mathematical expression that represents 'how many' of the circles, (or rectangles, for that matter), that we have above. That mathematical expression, again, looks like this:
3
This mathematical expression is made up of one mathematical element, the number 3. This mathematical expression evaluates to a value of 'three', (if a word is used), or '3', (if a number is used).
Mathematical expressions can have more than one number in them. They can also contain elements that are not numbers. For example, here is another mathematical expression:
3 + 2
This mathematical expression evaluates to a value of 'five' or '5'. Here is another mathematical expression that evaluates to a value of 'five' or '5':
5
Since both of these two newest expressions have the same value, they are equal expressions, and we can write:
3 + 2 = 5
Or:
5 = 3 + 2
One good way to think about a value is that it is a location on a number line. A number line is a line, drawn or imagined, with values strung along it. The value at any point can be indicated by a number called the coordinate of that point. As you move to the right along the number line the values get greater. They get less and less as you move to the left. A number line has a place called the origin; this is for the value of zero. Numbers to the right of zero are positive, numbers to the left of it negative.
Here's a picture of a number line:
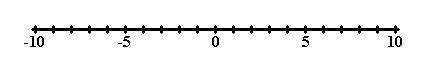
So, when two expressions are equal, then each of their values is located at the same spot on the number line.
Now, two expressions do not have to be equal. They could be unequal. In such a case one would find that after evaluating each expression separately to its corresponding value, then those two values would be located at different spots on the number line.
So, one expression can be greater in value or lesser in value than another, but for now, let's just deal with two expressions that are equal to each other.
Where are you?
Here: Introduction to Expressions
Other Representations Besides Numbers for Values
Introduction to Operators and Operands
More about Operators and Operands
And Now Including Variables and Functions
Just a Few Notes about Multiplication