Introduction to Operators and Operands

Back Expression Evaluation Math Science Contents Index Home

As we have seen, a mathematics expression can be made up of only one element, for example, a number, as in:

3

The above expression evaluates to three. This value of three can be represented by the number 3.

 

Usually, though, expressions are much more involved than the simple one above. Let's consider this one:

3 + 2

The above expression evaluates to five.

The above expression has three elements in it:

• The number 3
• The addition operator '+'
• The number 2

Well, we have already dealt with the idea that 2 and 3 are numbers representing values in an expression. Here, let's talk about the '+'.

Officially, the '+' in the above expression is called an operator. It is the addition operator.

Operators do not exist alone in expressions. That is, for example, the addition operator needs some values to add. It needs some values to operate upon.

In this expression:

3 + 2

The addition operator works with, or operates upon, the values represented by the numbers 3 and 2. The numbers 3 and 2 are said to be the operands for the '+', that is, the 3 and the 2 are operands for the addition operator.

 

It is very handy to think of the addition operator as 'grabbing' the 3 and the 2 and, through arithmetic, producing a value of five.

 

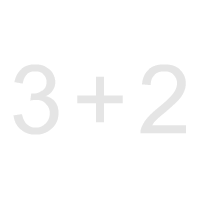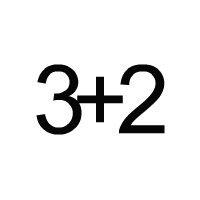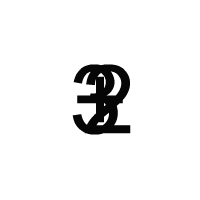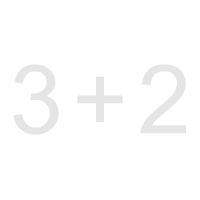
Speaking a bit more technically, we would say that the above expression evaluates to five because the addition operator operates on the 3 and the 2, (the number 3 and the number 2 are its operands), to produce a value of five.

So, now we know:

• Mathematics expressions are made up of operators and operands.
• When an expression is evaluated operators accept operands, (which are values), and produce new values through arithmetic.

Specifically, regarding the addition operator we see:

• The symbol for the addition operator is '+'.
• The addition operator needs two operands, one to its left and one to its right.
• The operands for the addition operator are values.

 

Since the addition operator requires two operands, we say that it is a binary operator. Binary means 'consisting of two parts'.

There are other binary operators present in expressions. There is also the subtraction operator, as in:

7 - 4

Here, the subtraction operator, '-', accepts the 7 and the 4, and using arithmetic it produces a value of three.

 

So, we now have two examples of binary operators in mathematics expressions:

• The addition operator, '+'
• The subtraction operator, '-'

 

Now, an expression can have several addition and subtraction operators in it. For example:

7 - 4 + 2

The operators are going to accept values as operands, but in this case, which operator gets the first turn at accepting these values, the '-' or the '+'?

To answer that question, it would be handy to know which operator is 'stronger'. In mathematics, when one operator is 'stronger' than another, we say that it has precedence over the other. That is, it precedes the other in the order of the steps taken necessary to evaluate the expression.

As it turns out the addition operator and the subtraction operator have equal precedence, one is not 'stronger' than the other. In cases like this, when two operators are of equal precedence, evaluation proceeds from left to right.

So, in this case the subtraction operator goes first since it is left most. In detail, here is how this evaluation unfolds, starting with the original expression:

7 - 4 + 2

The '-' operator goes first. It accepts the value of seven represented by the number 7 and the value of four represented by the number 4, does arithmetic called subtraction, and produces a value of three.

Since the value of three can be represented by the number 3, this work effectively changes the above expression to look like this:

3 + 2

Now, the action is handed over to the '+' operator. It accepts the value of three, (which was handed to it by the '-' operator), and the value of two represented by the number 2, does arithmetic called addition, and produces a value of five.

The value of five can be represented by the number 5, so the above expression boils down to this one:

5

 

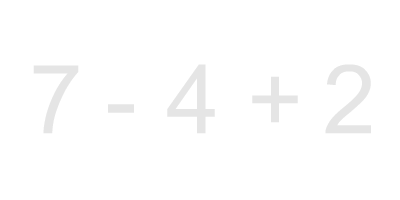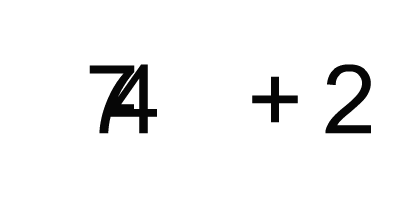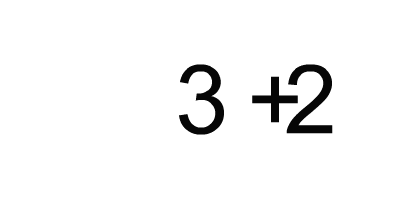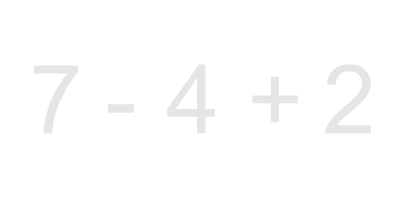
At this point we know:

• In math expressions there are operators and operands.
• It is the interaction among operators and operands that is called the evaluation of the expression.
• The evaluation of a mathematics expression produces a final value.
• Binary operators require two operands.
• The addition operator, '+', and the subtraction operator, '-', are both binary operators.
• The addition operator and the subtraction operator have equal precedence.
• When two operators have equal precedence, the one to the left accepts operands first, producing a value which is passed over to the other operator.

 

Where are you?

Introduction to Expressions

Other Representations Besides Numbers for Values

Here: Introduction to Operators and Operands

More about Operators and Operands

Unary Operations

Raise to a Power Operation

Parentheses

And Now Including Variables and Functions

Just a Few Notes about Multiplication

Terms and Factors

 

Back Expression Evaluation Math Science Contents Index Home