Expression Evaluation, Unary Operators

Not all operators in mathematics expressions are binary operators. Some are unary operators.

As you may guess, a unary operator accepts only one operand.

The positive sign and the negative sign are each unary operators. They accept only one value when they do arithmetic.

The positive sign looks a lot like the addition operator. For example, consider this expression:

+2

Is read 'positive two'. It does not really mean 'add two'.

What is happening here from an expression evaluation viewpoint is that the value of two represented by the number 2 is accepted as a single operand by the unary operator, '+', and that operation produces a value of positive two.

But, of course, the value of two represented by the number 2 is positive to start with, so, this operation is not too exciting.

Obviously, '+2' and '2' each represent the same value. So, one can say that an 'invisible' positive sign can be imagined before any number, (or variable or function, for that matter).

As mentioned above, the negative, (or opposite), sign is a unary operator. Consider this expression:

-3

Technically, here the negative sign operator accepts a value of three as its operand and produces a value of negative three.

Obviously, '-3' and '3' represent different values. There are no invisible negative signs in math expressions.

These two unary operations, '+' and '-', have precedence over all binary operations. To see this, let's look at a situation which is often termed a 'double negative' or stated as 'two negatives make a positive'. Consider this expression:

3 - -2

In this expression there are two operators that look like this: '-'. They are not the same. The first one, (left most), is the binary subtraction operator. The other, (right before the 2), is the unary negative sign operator.

From an expression evaluation viewpoint, things proceed as follows. The negative sign operator has precedence over the subtraction operator, so it accepts operands first. It accepts only one operand, since it is a unary operator. It accepts the value of two and produces a value of negative two. Now, the subtraction operator gets its chance to accept values. It takes the three and from it subtracts the negative two. This produces five, represented by the number 5, so we can write:

5 = 3 - -2

Now, this expression also equals five:

3 + 2

Since two expressions both equaling five equal each other we can write:

3 + 2 = 3 - -2

Although the expressions to the left and right of the equal sign above produce the same value, they each have quite a different story going on regarding the interaction of operators and operands.

So, the positive sign operator is not the addition operator, and the negative sign operator is not the subtraction operator.

But they look so much alike, those 'two negatives'! Or do they?

Actually, the positive sign operator is often differentiated from the addition operator by making it smaller and lifting it up a bit, as in:

⁺2 + ⁺3

Note:

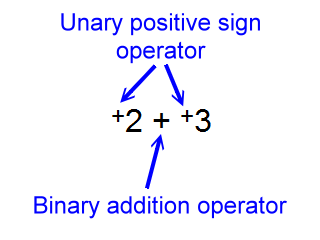
That would read 'positive two added to positive three'.

A similar visual difference is often used for the negative sign operator and the subtraction operator.

What was written above in the 'double negative' discussion:

3 - -2

Is much more clearly written this way:

3 - ^-2

Note:

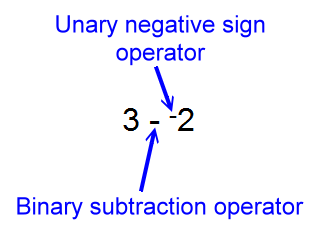
That makes it very clear that the negative sign is a different operator than the subtraction operator. This last expression would be read 'three subtract negative two'.

There is really no 'double negative' here. One operation is binary subtraction, the other is unary negation. The combination of these in like expressions may evaluate to a value equal to a similar looking expression involving an addition operator, and an addition operator may look like a positive sign, but it is really not the best mathematics to explain the fact that:

3 + 2 = 3 - ^-2

Using terms like 'double negative' or 'two negatives make a positive'.

So, is there ever a double negative or do two negatives ever make a positive?

Well, yes, if there really are two negative sign operators present, (and not one subtraction operator and one negative sign operator). It is unusual, though. Consider this expression:

^--2

Here there are two unary negative sign operators looking around, as we might say, for operands. They have equal precedence, so, which one accepts operands first?

Unlike the situation for binary operators where in situations of equal precedence evaluation proceeds from left to right, here, with unary operators of equal precedence evaluation goes from right to left.

 So, the value of two is accepted by the right most negative sign producing a value of negative two, or the opposite of two. This value is handed over to the left most negative sign producing the negative of negative two, or the opposite of the opposite of two, which is positive two.

In this case, then, it is fine to talk about double negatives and say that two negatives produce a positive. Now, with complete clarity we can write:

⁺2 = ^--2

But then, again, double negative signs are really not seen in most standard notation, but this thought might be useful when evaluating complicated math expressions.

Collecting a few ideas about expression evaluation:

• There are binary and unary operators.
• Unary operators have precedence over binary operators.
• Resolutions regarding binary operations of equal precedence proceed left to right.
• Resolutions regarding unary operations of equal precedence proceed right to left.

Where are you?

Introduction to Expressions

Other Representations Besides Numbers for Values

Introduction to Operators and Operands

More about Operators and Operands

Here: Unary Operations

Raise to a Power Operation

Parentheses

And Now Including Variables and Functions

Just a Few Notes about Multiplication

Terms and Factors