Expression Evaluation, Other Representations for Values besides Numbers
Now, let's just say that there are situations where one knows that a value exists, but one does not know exactly what that value is. For example, suppose you know that there are some salt shakers in this box:

How many salt shakers that are in that box is a value. (By the way, there may be zero salt shakers in that box.) That is, somewhere along the number line there is a spot that indicates the value for the number of salt shakers. But we don't know where that spot is.
However, none of this stops us from doing mathematics with the value of the number of salt shakers in this box. We just need to understand how to represent that value.
Symbols called variables are used to represent the concept of 'how many' when that concept is considered to exist, although the exact value of that concept may be unknown at the present, (and may continue to be unknown).
Well, let's just say that variables act like numbers, but you may not know which number that a variable is acting like.
Variables usually look like letters of the alphabet. So, if we want to do mathematics with the number of salt shakers in that box above, we need to decide upon a letter of the alphabet to represent the 'how many' for that value. Let's let the letter 'n' be that letter. Then we would say:
'Let n be the number of salt shakers in the box.'
If we wish to consider that there are three salt shakers in the box, then we would make statements like:
Let n equal 3.
Or:
Let n = 3.
Or simply:
n = 3
It is important to know, though, that we can do mathematics with the variable n without ever knowing how many salt shakers are in the box. For example, if the box doesn't weigh too much, it's possible to show that the total weight of it and its contents about doubles if the number of salt shakers inside of it doubles. One could find out that fact mathematically without ever knowing how many salt shakers were actually in the box.
So, values can be represented by numbers and variables.
Numbers are made up of digits and maybe a decimal point. Sometimes one considers a positive or negative sign part of a number. The value of a number is clearly represented by itself. Its location on the number line is not up to question.
Variables are symbols which are usually single letters of the alphabet. Variables are often called 'unknowns' because the exact value for a variable may be unknown in the problem you are facing. In fact, knowing the exact value of a variable may not actually enter into the work you are doing involving that variable. For example, this is true:
5 = 3 + 2
And this is true, too:
5 + n = 3 + 2 + n
The above statement is true no matter what the value for n may actually be. Here we have done some algebra using a symbol, n, for a value that is unknown.
So, we now have two methods for showing a value in a mathematics expression:
- Use a number, say, like 3.
- Use a variable, for example, n.
There is another manner in which a value can be introduced into a mathematics expression: the concept of a function. Currently, we will not go into depth regarding the definition of a function. As far as notation and algebra go, however, let's say that functions work in mathematics expressions much like a number or a variable.
The symbol for a function can have slightly different meanings in different contexts. Here, let's say that it is a symbol which represents a value.
A symbol for a function often looks like this:
f(x)
The above symbol is pronounced like this:
'f of x', ('ef of ex')
This entire symbol, f(x), acts like a value. That is, since this is true:
5 = 3 + 2
Then so is this true (adding f(x) to each side):
5 + f(x) = 3 + 2 + f(x)
What value does this symbol, f(x), represent? That is a good question! It's value can change, so it acts a bit like a variable. Actually, though, its value, called its output, is determined by what is known as its input. And the rule that ties the value of its output to the value of its input is called the definition of the function.
In the symbol f(x) the x stands for the input value. The name of the function is f. And the entire symbol, f(x), stands for the output value, that is, the value that enters the mathematics expression.
If we know the function definition, then we can determine the output value once we know the input value. For example, suppose the function is defined as:
f(x) = 5x
This states that the function will have a value, or output, equal to five times the input value. For example if 2 is input to this function, it will output 10. Starting again with the definition and placing a 2 in for the x, the math looks like this:
f(x) = 5x
f(2) = 5(2)
f(2) = 10
For the above we would say:
'f of two equals ten'
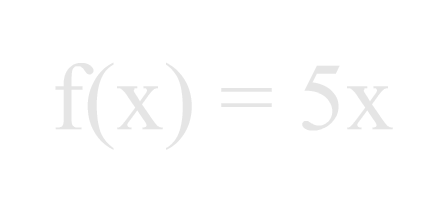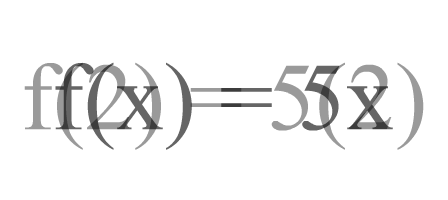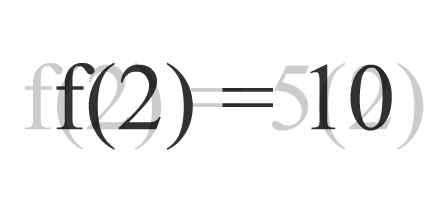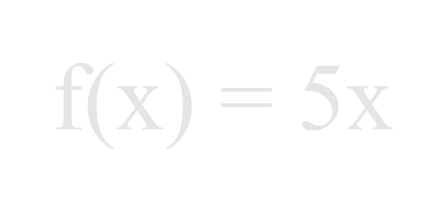
Of course, a different input would yield a different output. For example:
f(6) = 30
For the above we would say:
'f of six equals thirty'
Now, there is a lot more to understanding functions than this. They are mentioned here because it is important to understand the common ways in which values enter mathematics expressions right from the start when working with expression evaluation.
So, now we know that there are three common ways that values are represented in mathematics expressions:
- Numbers
- Variables
- Functions
Where are you?
Here: Other Representations Besides Numbers for Values
Introduction to Operators and Operands
More about Operators and Operands
And Now Including Variables and Functions