Expression Evaluation, Raise to a Power
Our final operator has the highest precedence, is binary, and is usually invisible. Here, we are going to discuss the raise to a power operation. Basically, a raise to a power operation looks like this:
23
The 2 is called the base. The 3 is called the exponent. The whole expression, that is, 23, is called the power. This power would be called 'the third power of two'. It is often also called 'two raised to the third power'. Just remember that, technically, the 3 is not the power. It's the exponent. Again, the power is 23.
This power, 23, evaluates to eight because 23 means two times itself three times, that is, two times two times two.
There is no visible operator. It is the positioning of the exponent, the 3 in this example, to the right and up from the base, the 2 in this example, that designates the operation.
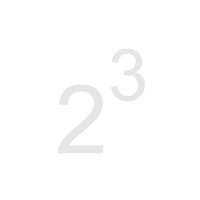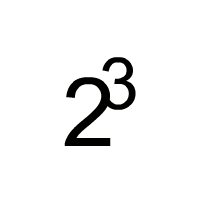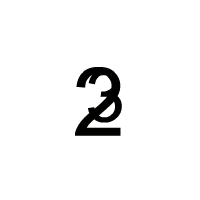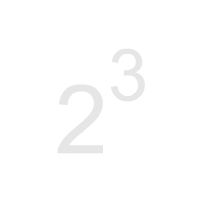
This raise to a power operation has precedence over all the binary operators (multiplication, division, addition, subtraction) and unary operators (positive and negative signs). For example, consider this example:
4 * 23
We have two operations present here: multiplication and raise to a power. The raise to a power operation goes first. So, two raised to the third power evaluates to eight, and then four times eight is thirty-two. Therefore, we can write:
32 = 4 * 23
Here is a harder one to understand:
-42
Now, the negative sign out front must wait till the raise to a power operation is finished. So, four raised to the second power is sixteen, since four times four is sixteen. After that evaluation the negative sign accepts the value of sixteen as an operand and produces a value of negative sixteen. Therefore, we can write:
-16 = -42
In other words, -42 does not mean negative four times negative four. That would be positive sixteen. Some calculators give this result; so, be careful and make sure that you understand how the calculator that you are using works.
The exponent may be negative. Consider this expression:
4-3
The negative sign on the exponent means that this power has the value of one divided by four raised to the third power. That is:
1 / 43 = 4-3
Although the above notation is not incorrect in any way, perhaps this is more clear:
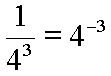
The exponent can be a fraction. Taking a root, such as a square root or a cube root, is actually the raising of a number to a fractional power. Here are some examples:
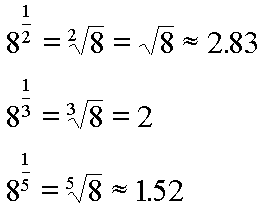
Now, if the exponent contains some arithmetic, all of that arithmetic must be done before you can clearly see with what power you are working. In other words, the exponent itself can be an expression with operators and operands. For example, consider this:
32 + 4
In the above example the exponent is the expression '2 + 4', which evaluates to six. So the entire expression, 32 + 4, evaluates to the sixth power of three, or equivalently three times three times three times three times three times three, or seven hundred and twenty nine. So:
32 + 4 = 36 = 729
Here is an interesting situation:
![]()
What does that mean? Well, it means 2 raised to some power. But what power? Well, the exponent for 2 contains some arithmetic which itself contains a raise to the power operation. The exponent for two is the fourth power of three, or eighty-one. In notation that looks this way:
![]()
By the way, the eighty-first power of two is quite a large number. My calculator reads: 2,417,851,639,229,258,349,412,352. I would suspect that is correct, but I really have no common experience to check it against.
Sometimes an operator is shown for the raise to the power operation. This is regularity true when such an expression must be entered into a device that does not permit superscripts, such as the graphics calculator like EZ Graph. Under such conditions a caret, or '^', is used. In other words, this:
3^4
Stands for this:
34
Where are you?
Other Representations Besides Numbers for Values
Introduction to Operators and Operands
More about Operators and Operands
Here: Raise to a Power Operation
And Now Including Variables and Functions
Just a Few Notes about Multiplication