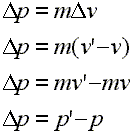Introductory Momentum Equations, Change in Momentum

Change in Momentum

On the previous page we looked at the quantity called impulse and noted that it was equal to a quantity called the change in momentum. The phrase 'impulse equals change in momentum' is a handy phrase worth memorizing. Here, we will look at several equations that present the change in momentum. Let us pick up by restating that the change in momentum, or delta p, is equal to the mass times the change in velocity, or delta v. Study the following four equations:

On the first line we state that the change in momentum is equal to the mass times the change in velocity.

In line two we change delta v to the quantity of the final velocity minus the original velocity, as one can do with any delta quantity.

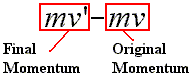
The mass is distributed over the two velocities on line three. Thus, the right side obviously ends up as the difference between two momenta. The momentum shown as the mass times the final velocity, i.e., mv', is the final momentum, and the momentum shown as the mass times the original velocity, i.e., mv, is the original momentum. So, on the right side of this third line we see the final momentum minus the original momentum.

On the fourth line we simply restate the change in momentum using the symbol p' for the final momentum and p for the original momentum.

Remember that the change in momentum of an object is equal to the impulse on the object. So, the last line above which states that the change in momentum is equal to the final minus the original momentum could be understood to state that the impulse on an object is equal to the final minus the original momentum.