Introductory Momentum Equations, Two Body Setup

Basic Setup for a Two Body Problem

Many situations include the interaction of two objects. For example, one object may be standing still, and another one that is moving collides with it. Or two objects may be driven apart by an internally generated force between them, perhaps provided by a spring. In such cases, as in all cases involving closed systems, momentum is conserved. That is, the momentum that is present in the system before the interaction is the exact amount of momentum present after the interaction, be it a collision or an explosion.

The analysis of any two body momentum problem usually starts with the same beginning equations. These first few equations all say the same thing: the total momentum of the system before the interaction is equal to the total momentum after the interaction. At first, we will think in only one dimension. Later, these same ideas will transfer over to more complicated problems involving two and three dimensional motion.

Here are the starting equations that can be used to understand momentum conservation in a two body problem. Study these three lines of equations and read the commentary below.

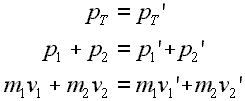
Line 1: Total momentum before equals the total momentum after. Line 2: Total momentum is expressed as the sum of the separate momenta. Line 3: Each separate momentum is expressed as the appropriate mass times the appropriate velocity.

The first line is true no matter how many objects are in the system. The total momentum of the system before any interaction is symbolized by p_T. After an interaction it is symbolized by p_T'. This total amount of momentum does not change in size or direction. After any interaction the same size of momentum in the same direction is present as was before. So, the first line is often quickly stated as 'the total momentum before is equal to the total momentum after.'

In the second line we show the total momentum as the sum of the separate momenta for each object in the system. We are discussing a two body system, so the subscript 1 refers to one of the objects, and the subscript 2 refers to the other. The sum of the separate momenta before an interaction equals the sum of the separate momenta after. Do not confuse this to mean anything like the momentum for the first object before the interaction equals the momentum for the first object after the interaction. Each object can, and will most likely, change its separate momentum. However, the sum total of all of the momenta before will equal the sum total of all of them after an interaction.

The third line simply states each separate momentum as the appropriate mass times the appropriate velocity for each object. Most two body problems proceed from here by entering values or considering special conditions from this line onward. Check the examples on the following pages to see how this works.