Introductory Momentum Equations, Two Body, Push Apart

Push Apart Problem

Suppose that two objects are standing still, and a spring between them drives them apart. One object would be sent out to left and the other sent out to the right. As in any closed system, momentum would be conserved.

It is important to understand that the total momentum before the interaction is zero. Therefore, after the two objects are pushed apart, the total momentum is still zero. However, each object, if considered separately, has a non-zero momentum. That is because each object is in motion. How can this be? The total momentum afterwards is zero, yet both objects are moving?

The object moving off to the left has a negative momentum, while the object moving to the right has a positive momentum. These two momenta are equal and opposite, so, when they are added together to calculate the total momentum afterwards, they cancel each other. That is how both objects can be in motion, yet the total momentum is zero. For example, the first object, moving to the left afterwards, might have a final momentum of -6 kg-m/s. This would mean that the second object, moving to the right afterwards, would have a final momentum of 6 kg-m/s.

Now, just because their final momenta are equal and opposite, their final velocities are not necessarily equal and opposite. For their final velocities to be equal and opposite, their masses would have to be equal. That is a special case. In a general case, in this situation, the object with the more mass will move slower afterwards than the one with less mass. Therefore, the final momentum of the first object would be negative and might be calculated by multiplying a large mass times a small velocity; the final momentum of the second object would be positive and would be calculated by multiplying a small mass times a large velocity.

These are the equations for this situation:

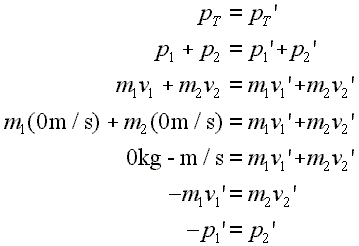
Lines 1, 2, and 3: Basic start for two body problem. Line 4: Original velocities for both objects are set to zero. Line 5: Left side of equation becomes zero, since original velocities are zero. Line 6: Algebra rearrangement. Line 7: Restatement of line 6, using the symbol for momentum rather than mass times velocity.

Once more, the first three lines are the basic setup for a two body momentum problem.

Line four shows that the two bodies are standing still before they are pushed apart. That is, both of their original velocities are zero.

Of course, as seen in line five, if the objects are not moving before the interaction, then the total momentum will at that point be zero.

Line six shows that the velocity that after the push apart the first object ends up with a momentum that is equal and opposite to that of the second object. In other words, the size of the momentum that the first object moves off with to the left is the same size as the momentum that the second object moves off with to the right.

Line seven restates line six, but replaces the products of mass times velocity with symbols for momentum. Notice again that in this situation after the push apart the momentum of the first object is equal and opposite to that of the second.