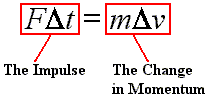Introductory Momentum Equations, Impulse
![]() Impulse
Impulse
Impulse is an important concept in the study of momentum. Time passes as a force is applied to an object. When this happens we say that an impulse is applied to the object. For example, when a tennis racket strikes a tennis ball, an impulse is applied to the ball. The racket puts a force on the ball for a short time period. By the way, according to Newton's third law of motion, forces come in pairs. So, the ball also puts a force on the racket, and the racket, therefore also has an impulse applied to it.
|
Forces applied over time periods create impulses. |
An impulse is equal to the net force on the object times the time period over which this force is applied. Below, we derive impulse from the equation F = ma, which comes from Newton's second law of motion. Study the following three lines and read the commentary under them.
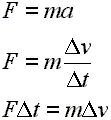
|
Line 1: Force equals mass times acceleration. Line2: Definition of acceleration. Line 3: Algebraic rearrangement, the force multiplied by the time period equals the mass multiplied by the change in velocity. |
The first line is our familiar equation F = ma.
The second line expresses the acceleration as the change in velocity divided by the change in time. This is the basic definition of acceleration.
The third line is arrived at through algebra by multiplying each side of the equation by delta t, canceling it on the right, effectively moving it over to the left.
|
|
The left side of the third line is called the impulse on the object. That is, impulse
is equal to the
net force times the length of time over which that force is applied.
The right side of the third line is called the change in momentum. So, we say the impulse equals the change in momentum. More about the change in momentum later. For now, we will take a closer look at the impulse. |
|
The impulse equals the change in momentum. |
Below is a sample calculation for impulse. Imagine that a force of 2.0 N is applied to an object for 3.0 s. Here is how to calculate that impulse:
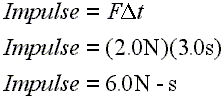 |
Line 1: Definition of impulse. Line 2: Enter example values for force and time period. Line 3: Calculate the resultant impulse. |
Notice that impulse is measured in N-s (pronounced "Newton seconds") and that change in momentum is measured in kg-m/s (pronounced "kilogram meter per second"). Since the above derivation shows that an impulse is equal to a change in momentum, these two units must be equivalent, and they are.
First, remember that mass units are kilograms, and that acceleration units are meter per second squared:
kilogram → Unit for mass → kg
meter per second squared → Unit for acceleration → m/s2
Remember that a Newton is a kilogram-meter per second squared:
Newton → Unit for force → F = ma → N = kg × m/s2 → kg-m/s2
N → kg-m/s2 → (kg × m) / (s × s)
Then hopefully this diagram will show you that an impulse unit (N-s) is equivalent to a momentum unit (kg-m/s):
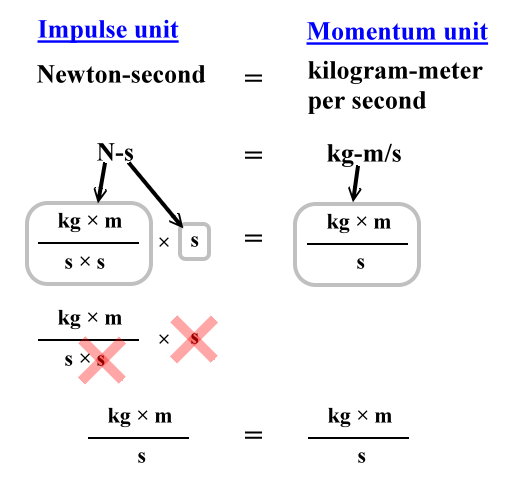
Usually, if one is discussing momentum or changes in momentum, one uses the kg-m/s unit. If impulse is under discussion, then N-s is commonly used. However, there is really nothing wrong with interchanging the use of these units.
Here's some multiple-choice problems that you can use to check your understanding: