Parabola Transformations

In this section we will be explaining several transformations demonstrated with a simple second degree polynomial function, the parabola. Below the following animation you will find some introductory information about these transformations, and to the right of the animation there are several links leading to further material for this section.

We will need a basic, bare-bones parabolic function from which we can relate our scaling and translating transforms. That function is:

y = x²

The graph for the above function will act as a reference from which we can describe our transforms. The graph of y = x² looks like this:

We will call this our reference parabola, or, to generalize, our reference function. We will talk about our transforms relative to this reference parabola.

So, for example, if we speak about a so called horizontal translation of this parabola, we are describing how many units to the left or right this parabola has moved across the graph paper.

If, for another example, we are talking about vertical scaling, then we are stating how much this reference parabola has been vertically stretched or compressed.

We will look at other transforms also. In each case the transform will have a name and value that describe a change in the reference parabola that moves or flexes it in order to create a new, transformed parabola. We want to know how to do this by looking at the equation for the transformed parabola.

In the graph below we imagine that the reference parabola, shown in transparent light gray, has been moved to a new position eight units to the right, there shown in solid black.

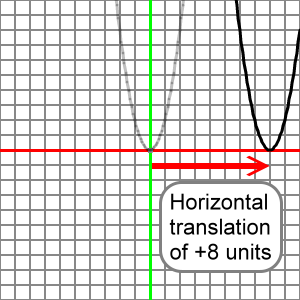
We would say that this solid black parabola has undergone a transform that is a translation of positive eight units to the right. Or we could describe this as a horizontal translation of plus eight units, or we could say this is an x-translation of 8.

Now that we understand the concept of the reference parabola, or reference function, let's take a look at several transforms that can stretch, squash, flip, and move our simple parabolic function, y = x². First, we will look at vertical scaling and cover vertical reflections along the way. Next, we will move through vertical and horizontal translations. We will not cover horizontal scaling or horizontal reflections for the parabola.